Chọn đáp án C
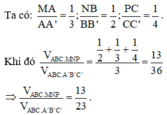
Chú ý: Trong bài toán trên ta sử dụng công thức tính nhanh sau:



Chọn đáp án C


Chú ý: Trong bài toán trên ta sử dụng công thức tính nhanh sau:



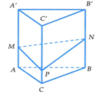
Cho lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm các cạnh A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chưa điểm B có thể tích là V 1 . Gọi V là thể tích khối lăng trụ. Tính V 1 V .
A. 25 288
B. 29 144
C. 37 288
D. 19 144
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA'=4A'M , BB'=4B'N Mặt phẳng (C'MN) chia khối lăng trụ thành hai phần. Gọi V 1 là thể tích khối chóp C’.A’B’MN và V 2 là thể tích khối đa diện ABCMNC’. Tính tỷ số V 1 V 2
A. V 1 V 2 = 1 5
B. V 1 V 2 = 4 5
C. V 1 V 2 = 2 5
D. V 1 V 2 = 3 5
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 là phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB',CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B , V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Cho lăng trụ ABC.A'B'C' trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA'=3A'M , BB'=3B'N Mặt phẳng (C'MN) chia khối lăng trụ đã cho thành hai phần. Gọi V 1 là thể tích của khối chóp C'.A'B'MN, V 2 là thể tích của khối đa diện ABCMNC' Tỉ số V 1 V 2 bằng:
A. V 1 V 2 = 4 7
B. V 1 V 2 = 2 7
C. V 1 V 2 = 1 7
D. V 1 V 2 = 3 7
Cho khối lăng trụ ABC.A'B'C' . Gọi M là trung điểm của BB' , N là điểm trên cạnh CC' sao cho C N = N C ' . Mặt phẳng ( AMN ) chia khối lăng trụ thành hai phần có thể tích V1 và V2 như hình vẽ. Tính tỉ số V 1 V 2 .
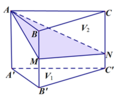
A. V 1 V 2 = 5 3 .
B. V 1 V 2 = 3 2 .
C. V 1 V 2 = 4 3 .
D. V 1 V 2 = 7 5 .
Cho lăng trụ A B C A ' B ' C ' , trên cạnh AA';BB' lấy các điểm M, N sao cho A A ' = 3 A ' M ; B B ' = 3 B ' N . A A ' = 3 A ' M ; B B ' = 3 B ' N Mặt phẳng chia khối lăng trụ đã cho thành hai phần. Gọi V 1 là thể tích khối chóp C'A'B'NM , V 2 là thể tích khối đa diện ABC.MNC'. Tính tỉ số V 1 V 2
A. 2 9
B. 3 4
C. 2 7
D. 5 7
Cho khối lăng trụ tam giác A B C . A ' B ' C ' . Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai khối đa diện. Gọi V 1 là thể tích của khối đa thức diện chứa đỉnh B và V 2 là thể tích khôi đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA’, BB’, CC’ sao cho A M = 2 M A ' , N B ' = 2 N B , P C = P C ' . Gọi V 1 , V 2 lần lượt là thể tích của hai khối đa diện A B C M N P và A’B’C’MNP. Tính tỉ số V 1 V 2 .
A. V 1 V 2 = 2.
B. V 1 V 2 = 1 2 .
C. V 1 V 2 = 1.
D. V 1 V 2 = 2 3 .