Các câu hỏi tương tự
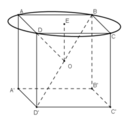
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.
Tính bán kính của đường tròn là giao tuyến của mp(ABCD) với mặt cầu trên.
Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật. Tâm của mặt cầu (S) là:
A. Tâm của hình hộp chữ nhật
B. Tâm của một mặt bên của hình hộp chữ nhật
C. Trung điểm của một cạnh của hình hộp chữ nhật
D. Một đỉnh bất kì của hình hộp chữ nhật
Một hình hộp chữ nhật có ba kích thước là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tâm của mặt cầu (S) là
A. Một đỉnh bất kì của hình hộp chữ nhật.
B. Tâm của một mặt bên của hình hộp chữ nhật.
C. Trung điểm của một cạnh của hình hộp chữ nhật.
D. Tâm của hình hộp chữ nhật.
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , B C = a Biết bán kính của mặt cầu ngoại tiếp của hình hộp chữ nhật là 3 a 2 Thể tCho hình hộp chữ nhậích của hình hộp chữ nhật là
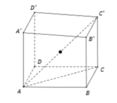
A. a 3 3 2
B. 4 a 3
C. 2 a 3
D. 2 3 a 3
Cho hình hộp chữ nhật ABCD.ABCD có các kích thước là AB2, AD3, AA4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABBA và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có các kích thước là AB=2, AD=3, AA'=4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB'A' và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:
Đi qua 8 đỉnh của hình lập phương.
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AD2a, AA3a. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.ABCD là
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AD=2a, AA'=3a. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là
![]()
![]()
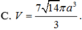
![]()
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a, AD 2a và AA’ 3a. Bán kính mặt cầu ngoại tiếp tứ diện ACB’D’ là: A.
a
3
2
B.
a
3
4
C.
a
14
2
D.
a
6...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD = 2a và AA’ = 3a. Bán kính mặt cầu ngoại tiếp tứ diện ACB’D’ là:
A. a 3 2
B. a 3 4
C. a 14 2
D. a 6 2
Cho hình hộp ABCD.ABCD có AB AD 2a, AA 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.ABCD nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích
V
T
V
C
giữa khối cầu và khối trụ là.
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có AB = AD = 2a, AA' = 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.A'B'C'D' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V T V C giữa khối cầu và khối trụ là.
![]()
![]()
![]()