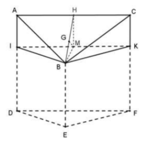

Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và B H = 3 2 a
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC

Chọn B


Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và B H = 3 2 a
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC

Chọn B
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng ∆ đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E, F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng ∆ cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu?
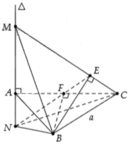
A. a 3 6 4 .
B. a 3 3 4 .
C. a 3 3 6 .
D. a 3 6 12 .
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh, a góc giữa mặt bên và mặt phẳng đáy là α thoả mãn cos α = 1 3 . Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị nào trong các giá trị sau
A. 0,11
B. 0,13
C. 0,7
D. 0,9
Cho tam giác ABC vuông tại A.Điểm D trên cạnh AC sao cho CD=2AD.Lấy điểm E trên đoạn thẳng BD thỏa mãn góc CED bằng góc ABC.Gọi F là điểm đối xứng của B qua A.Giao điểm BD và CK là điểm M.Chứng minh rằng :
a,Tứ giác AMCB là hình thangb,Tam giác AMB đồng dạng với tam giác EBC.c,EF.MC=CB.BEd, Góc DEF bằng 2 lần góc ABCCho tam giác OAB đều cạnh a. Trên đường thẳng d qua O và vuông góc với mặt phẳng (OAB) lấy điểm M sao cho O M = x . Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB. Gọi N là giao điểm của EF và d. Tìm x để thể tích tứ diện ABMN có giá trị nhỏ nhất.
A. x = a 2
B. x = a 2 2
C. x = a 3 2
D. x = a 6 12
Cho hình chóp .S ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( A B C ) , B C = a , góc hợp bởi (SBC) và SBC) là 60 0 Mặt phẳng (P) qua A vuông góc với SC cắt SB, SC lần lượt tại D, E. Thể tích khối đa diện ABCED là
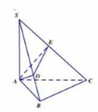
A. a 3 3 6
B. 11 a 3 3 120
C. 11 a 3 3 60
D. 3 a 3 3 40
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a, A C = a 3 , tam giác SAB đều và nằm trong mặt phẳng vuông góc đáy. Gọi a (độ) là bởi cạnh SB và mặt phẳng (SAB). Gía trị a gần với số nào nhất dưới đây?
A. 30
B. 40
C. 50
D. 60
Cho tam giác OAB đều cạnh a. Trên đường thẳng d qua O và vuông góc với mặt phẳng (OAB) lấy điểm M sao cho OM=x. Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB. Gọi N là giao điểm của EF và OM. Tìm x để thể tích tứ diện ABMN có giá trị nhỏ nhất
A. x = a 2 .
B. x = a 2 2 .
C. x = a 6 12 .
D. x = a 3 2 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = A , B C = A 3. Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng 5 a 2 3 2 . Tính theo a khoảng cách d từ A đến mặt phẳng (SBC) gần với giá trị nào nhất sau đây ?
A. 0,72 a
B. 0,90a
C. 0,80a
D. 1,12a
Cho hình lăng trụ ABC A'B'C' có AA'=a, góc giữa cạnh bên và mặt đáy bằng 60°. Tam giác ABC vuông tại C và góc B A C ^ = 60 ° . Hình chiếu vuông góc của B' lên mặt phẳng A B C trùng với trọng tâm của Δ A B C . Tính thể tích khối tứ diện A'ABC theo a
A. V A ' A B C = 3 a 3 208
B. V A ' A B C = 27 a 3 208
C. V A ' A B C = 81 a 3 208
D. V A ' A B C = 9 a 3 208