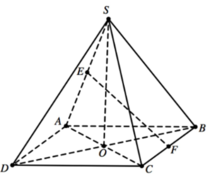
Chọn gốc toạ độ tại O = A C ∩ B D các tia Ox, Oy, Oz lần lượt trùng với các tia OC, OB, OS. Ta có O(0;0;0), A - 2 2 ; 0 ; 0 , B 0 ; 2 2 ; 0 C 2 2 ; 0 ; 0 , D 0 ; - 2 2 ; 0 , S(0;0;h)
Khi đó
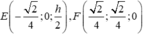

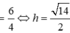
Do đó
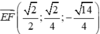
![]()
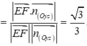
Chọn đáp án A.
Chọn gốc toạ độ tại O = A C ∩ B D các tia Ox, Oy, Oz lần lượt trùng với các tia OC, OB, OS. Ta có O(0;0;0), A - 2 2 ; 0 ; 0 , B 0 ; 2 2 ; 0 C 2 2 ; 0 ; 0 , D 0 ; - 2 2 ; 0 , S(0;0;h)

Khi đó
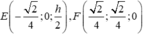

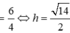
Do đó
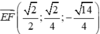
![]()
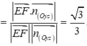
Chọn đáp án A.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a tâm O. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng 60 ° . Tính cosin góc giữa đường thẳng và mặt phẳng (SBD)
A. 41 41
B. 5 5
C. 2 5 5
D. 2 41 41
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 2 .
B. 3
C. 2
D. 1
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng S B D , tan α bằng
A. 2
B. 3
C. 2
D. 1
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SA và BC. Biết góc giữa MN và mặt phẳng (ABCD) bằng 60 0 . Khoảng cách giữa hai đường thẳng BC và DM là:
A. a 15 62
B. a 30 31
C. a 15 68
D. a 15 17
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của BC, SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 1
B. 2
C. 2
D. 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong một mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của các cạnh AB và AD. Tính sin của góc tạo bởi giữa đường thẳng SA và mặt phẳng (SHK)
A. 2 2
B. 2 4
C. 7 4
D. 14 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của các cạnh AB, AD. Tính sin của góc tạo bởi giữa đường thẳng SA và (SHK).
A. 2 2
B. 2 4
C. 14 4
D. 7 4
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng
A. 60 0 .
B. 90 0 .
C. 45 0 .
D. 75 0 .
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và A B = 2 a , B C = a . Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là:
A. a 3 3
B. a 6 3
C. a 15 5
D. a 21 7