Các câu hỏi tương tự
cho hình chóp S.MNP có đáy MNP là tam giác đều. Gọi E,F,G lần lượt là trung điểm SM,SN,SP. a) tìm hình chiếu song song của đoạn thẳng EF,EG trên (MNP) qua phép chiếu theo phương SPb) tìm hình chiếu song song của tam giác EFG trên (MNP) qua phép chiếu theo phương SP
Đọc tiếp
cho hình chóp S.MNP có đáy MNP là tam giác đều. Gọi E,F,G lần lượt là trung điểm SM,SN,SP.
a) tìm hình chiếu song song của đoạn thẳng EF,EG trên (MNP) qua phép chiếu theo phương SP
b) tìm hình chiếu song song của tam giác EFG trên (MNP) qua phép chiếu theo phương SP
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết Tính thể tích V của khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết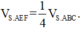 
Tính thể tích V của khối chóp S.ABC
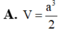
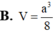
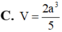
cho hình chóp S.ABC có đáy ABC là tam giác đều. Gọi M,N,P lần lượt là trung điểm SA,SB,SC.
tìm hình chiếu song song của đoạn thẳng NP trên (ABC) qua phép chiếu theo phương SA
Cho hình chóp SABCD có đáy ABCD là tứ giác lồi. Lấy điểm M trên cạnh SA sao cho SM = 1/2 SA, điểm N trên cạnh CD sao cho CN =1/2 CD, điểm P trên cạnh SB sao cho SP = 3/4 SD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP)
cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm o gọi M,N lần lượt nằm trên SA ,SC sao cho SM=MA, SN=1/3 SC Gọi I K lần lượt là hình chiếu song song của điểm M , N trên mặt phẳng (ABCD) theo phương SO. tính OK/OI
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các đoạn SB, SD. Lấy điểm P trên cạnh SC sao cho SP = 3SC. Tìm giao tuyến của mp ( MNP ) với các mp (SAC), (SAB), (SAD), (ABCD)
Cho hình chóp tứ giác đều S.BACD có cạnh đáy bằng a. Các điểm M; N; P lần lượt là trung điểm của SA; SB; SC. Mặt phẳng (MNP) cắt hình chóp theo 1 thiết diện có diện tích bằng? A.
a
2
B.
a
2
2
C.
a
2
4
D.
a
2
8
Đọc tiếp
Cho hình chóp tứ giác đều S.BACD có cạnh đáy bằng a. Các điểm M; N; P lần lượt là trung điểm của SA; SB; SC. Mặt phẳng (MNP) cắt hình chóp theo 1 thiết diện có diện tích bằng?
A. a 2
B. a 2 2
C. a 2 4
D. a 2 8
Cho hình chóp S.ABCD. Hai điểm M và G lần lượt là trọng tâm tam giác SAB và SAD; điểm N thuộc SG và P nằm trong tứ giác ABCD. Gọi I; J lần lượt là trung điểm của AB và AD và K là giao điểm của MN và IJ; E là giao điểm của KP và AC; F là giao điểm của IJ và AC Tìm giao tuyến của (MNP) và (SAC) A. EF B. KE C. KF D. Tất cả sai
Đọc tiếp
Cho hình chóp S.ABCD. Hai điểm M và G lần lượt là trọng tâm tam giác SAB và SAD; điểm N thuộc SG và P nằm trong tứ giác ABCD. Gọi I; J lần lượt là trung điểm của AB và AD và K là giao điểm của MN và IJ; E là giao điểm của KP và AC; F là giao điểm của IJ và AC Tìm giao tuyến của (MNP) và (SAC)
A. EF
B. KE
C. KF
D. Tất cả sai
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn SM
1
4
SA, SN
1
3
SB, SP 3SC. Thể tích của khối chóp S.MNP theo V
A
.
V
5
B
.
V
4
C
.
V
3
D...
Đọc tiếp
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn SM = 1 4 SA, SN = 1 3 SB, SP = 3SC. Thể tích của khối chóp S.MNP theo V
A . V 5
B . V 4
C . V 3
D . V 2