Đáp án B
Do A D / / B C
Do đó \ I B C ∩ S A D = IJ ⇒ I J / / A D / / B C
Đáp án B

Do A D / / B C
Do đó \ I B C ∩ S A D = IJ ⇒ I J / / A D / / B C
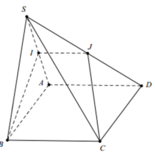
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I là trung điểm của SA, thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là
A. Tam giác IBC.
B. Hình thang IJCB (J là trung điểm SD ).
C. Hình thang IGBC (G là trung điểm SB ).
D. Tứ giác IBCD
Cho hình chóp S.ABCD có đáy ABCD là hình thang AB//CD. Gọi I, J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB. Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng?
A. AB=3CD
B. A B = 1 3 C D
C. A B = 3 2 C D
D. A B = 2 3 C D
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là trung điểm của cạnh SA, F, G là các điểm thuộc cạnh SC, AB (F không là trung điểm của SC). Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là:
A. Lục giác
B. Tứ giác
C. Ngũ giác
D. Tam giác
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Cạnh bên SA vuông góc với đáy, S A = 2 a 3 . Gọi I là trung điểm của mặt phẳng (P) đi qua I và vuông góc với SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
A. 3 5 16 a 2
B. 3 15 16 a 2
C. 15 3 16 a 2
D. 5 3 16 a 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì
A. AB = 3CD
B. AB = 2CD
C. CD = 3AB
D. CD = 2AB
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SB. Thiết diện của mặt phẳng (ADM) với hình chóp là
A. Hình thang
B. Hình bình hành
C. Tam giác
D. Hình thang hoặc hình tam giác
Cho hình chóp S.ABCDcó đáy ABCD là hình thang đáy AB,AB=2DC Gọi M, N là trung điểm của SA và SD. Tính tỉ số thể tích của hai hình chóp V S . B C N M V S . B C D A
A. 1 4
B. 5 12
C. 3 8
D. 1 3
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh SA=2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và α là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng với hình chóp S.ABCD là
A. S = a 2
B. S = 3 a 2 2
C. S = a 2 2
D. S = 2 a 2
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC; A D = 3 B C = 3 a ; A B = a , S A = a 3 . Điểm I thỏa mãn A D ⇀ = 3 A I ⇀ ;M là trung điểm SD, H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , . SC Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).
A. V = πa 3 2 5
B. V = πa 3 5
C. V = πa 3 10 5
D. V = πa 3 5 5