Question

cho hình chóp S.ABCD, đáy ABCD là hình bình hành, tâm O. Gọi M là trung điểm SD

a) vẽ hình

b) xét vị trí tương đối của OM và (SBD)

c) chứng minh OM ∥ (SBA)

d) chứng minh OM ∥ (SBC)

e) chứng minh SB ∥ (MAC)

f) tìm giao tuyến của (OMA) và (SAB)

Answer 1

a: 

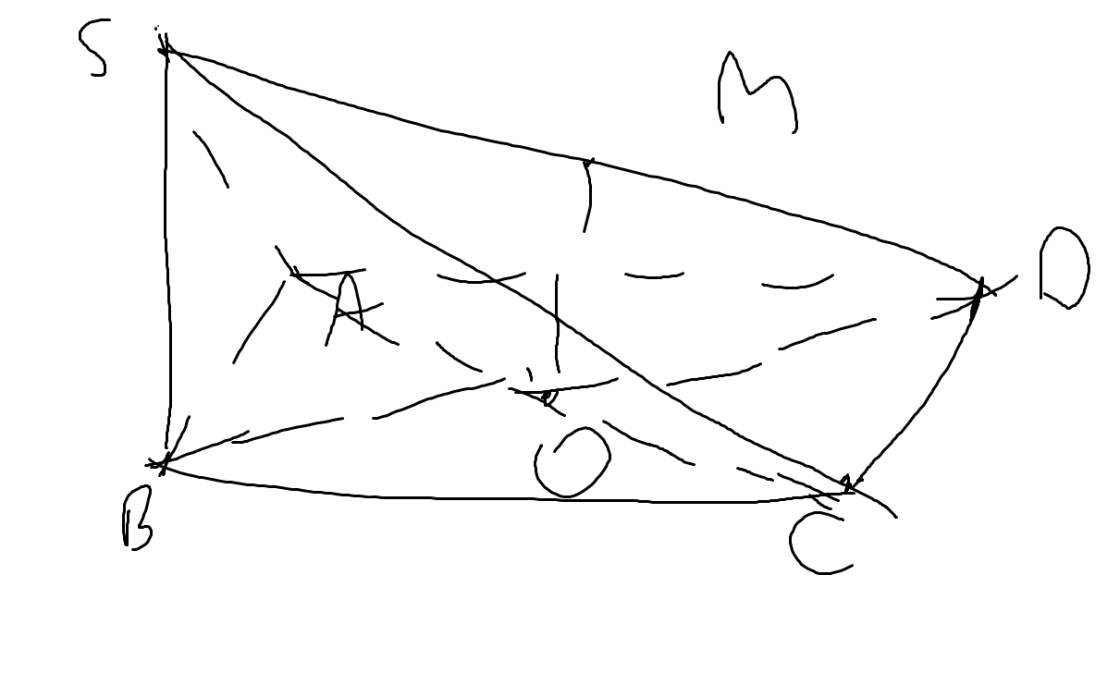
b: \(O\in BD\subset\left(SBD\right);M\in SD\subset\left(SBD\right)\)

=>\(OM\subset\left(SBD\right)\)

c: Xét ΔDSB có

O,M lần lượt là trung điểm của DB,DS

=>OM là đường trung bình của ΔSDB

=>OM//SB

OM//SB

\(SB\subset\left(SBA\right)\)

OM không nằm trong mp(SBA)

Do đó: OM//(SBA)

d: OM//SB

\(SB\subset\left(SBC\right)\)

OM không nằm trong(SBC)

Do đó: OM//(SBC)

e: SB//MO

\(MO\subset\left(MAC\right)\)

SB không nằm trong mp(AMC)

Do đó: SB//(MAC)

f: Xét (OMA) và (SAB) có

\(A\in\left(OMA\right)\cap\left(SAB\right)\)

OM//SB

Do đó: (OMA) giao (SAB)=xy, xy đi qua A và xy//OM//SB