Đáp án C
Dựng A H ⊥ B D , lại có
S A ⊥ S H A ⇒ S B D ; A B C D ^ = S H A ^
Ta có A H = 2 a 5 ⇒ tan α = S A A H = 15 2

Đáp án C
Dựng A H ⊥ B D , lại có
S A ⊥ S H A ⇒ S B D ; A B C D ^ = S H A ^
Ta có A H = 2 a 5 ⇒ tan α = S A A H = 15 2
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
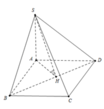
Cho hình chóp S.ABCD có S A ⊥ A B C D , ABCD là hình chữ nhật có A B = a , A D = 2 a , S A = a 3 . Tính tan của góc giữa hai mặt phẳng (SBD) và (ABCD).
A. 2 5 5
B. 3 5 2
C. 15 3
D. 15 2
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB =a, BC =2a, B D = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 độ. Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết A B = a , B C = 2 a , B D = a 10 Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 ° . Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên đáy ABCD trùng với trung điểm AB. Biết A B = a , B C = 2 a , B D = a 10 . Góc giữa hai mặt phẳng (SBD) và đáy là 60 ° . Tính d là khoảng cách từ A đến mặt phẳng (SCD) gần với giá trị nào nhất trong các giá trị sau đây ?
A. 0,80a
B. 0,85a
C. 0,95a
D. 0,98a
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; A B = B C = 1 , A D = 2. Các mặt chéo S A C và S B D cùng vuông góc với mặt đáy A B C D . Biết góc giữa hai mặt phẳng S A B và A B C D bằng 60 0 (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng S A B là
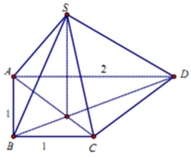
A. 2 3 3
B. 3
C. 2 3
D. 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=a , AD=2a Cạnh bên SA vuông góc với đáy (ABCD), SA=2a Tính tan của góc giữa hai ămtj phẳng (SBD) và (ABCD)
A. 1 5
B. 2 5
C. 5
D. 5 2
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD).
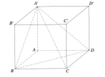
A. 5 91 49
B. 3 14 49
C. 9 14 98
D. 11 70 98