Đáp án B
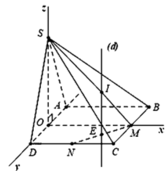
Xét trục tọa độ Oxyz như hình vẽ, với O là trung điểm của AD
Chọn a = 1 => 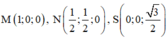 => Trung điểm của MN là
=> Trung điểm của MN là 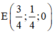
Phương trình đường thẳng qua E, song song với Oz là 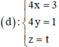
Gọi I là tâm mặt cầu cần tìm => 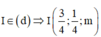
Suy ra 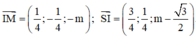
Mà 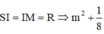
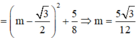
Vậy 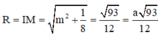
Đáp án B

Xét trục tọa độ Oxyz như hình vẽ, với O là trung điểm của AD
Chọn a = 1 => 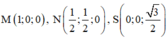 => Trung điểm của MN là
=> Trung điểm của MN là 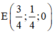
Phương trình đường thẳng qua E, song song với Oz là 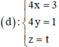
Gọi I là tâm mặt cầu cần tìm => 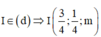
Suy ra 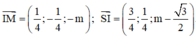
Mà 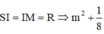
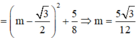
Vậy 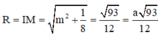
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CMN
A. R = 5 a 3 12 .
B. R = a 29 8 .
C. R = a 93 8 .
D. R = a 37 6 .
Cho hình chop S.ABCD có đáy hình vuông cạnh 1, tam giác SAD là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm của BC và CD. Tính bán kính R của khối cầu ngoại tiếp hình chop S.CMN
A. R = 29 8
B. R = 5 3 12
C. R = 39 12
D. R = 37 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Bán kính của mặt cầu ngoại tiếp hình chóp S.CMN là:
A. a 93 12
B. a 29 8
C. 5 a 3 12
D. a 37 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Tính thể tích khối chóp S.CMN.
A. V = a 3 3 18
B. V = a 3 3 24
C. V = a 3 3 48
D. V = a 3 3 8
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh 2a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm của BC và CD. Khi đó bán kính mặt cầu ngoại tiếp khối SCMN là:
A. 3 a 2
B. a 3
C. 93 6 a
D. 31 12 a
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật; AB=a,AD=2a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD
A. R = 3 a 2 2
B. R = 2 a 2 3
C. R = 2 a 3 3
D. R = 3 a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với 𝐴𝐵=𝐴𝐷=1, 𝐶𝐷=2. Cạnh bên SD vuông góc với mặt đáy, còn cạnh bên SA tạo với mặt đáy một góc 45°. Gọi E là trung điểm của cạnh CD. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.BCE.
A. R = 3 2
B. R = 14 2
C. R = 5 2
D. R = 11 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với A B = a , B C = a 3 . Cạnh SA vuông góc với mặt phẳng đáy và S A = 2 a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC
A. R = a
B. R = 3a
C. R = 4a
D. R = 2a
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc B A D ^ = 120 ° . Cạnh bên SA vuông góc với đáy (ABCD) và SA = 3a. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.BCD
A. 3 a 3
B. 5 a 3
C. 5 a 3
D. 4 a 3