Các câu hỏi tương tự
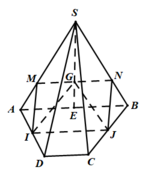
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành? A. AB3CD B. AB2CD C. CD2AB D. CD3AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp ![]() cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?
cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?

A. AB=3CD
B. AB=2CD
C. CD=2AB
D. CD=3AB
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (GIJ) với hình chóp S.ABCD là hình bình hành.
A. AB = CD
B. AB = 3CD
C. 3AB = CD
D. AB = 2CD
Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm tam giác SAB. Tìm thiết diện của hình chóp S.ABCD cắt bởi (IJG) A. Thiết diện là tam giác GIJ. B. Thiết diện là hình thang MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB. C. Thiết diện là hình bình hành MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB. D. Thiết...
Đọc tiếp
Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm tam giác SAB. Tìm thiết diện của hình chóp S.ABCD cắt bởi (IJG)
A. Thiết diện là tam giác GIJ.
B. Thiết diện là hình thang MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB.
C. Thiết diện là hình bình hành MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB.
D. Thiết diện là tam giác KIJ, với K là giao điểm của GI với SB.
Cho hình chóp S.ABCD có đáy ABCD là hình thang(hai cạnh đáy là AB,CD). Gọi I,J lần lượt là trung điểm của các cạnh AD,BC và G là trọng tâm của ΔSAB. Tìm k để AB=k*CD để thiết diện của mặt phẳng (GIJ) với hình chóp S.ABCD là hình bình hành
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB và CD. Gọi I ,J lần lượt là trung điểm của AD và BC, G là trọng tâm của tam giác SAB. Tìm giao tuyến của hai mặt phẳng (SAB) và (IJG).
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm khẳng định đúng A. giao tuyến của (SAB) và (IJG) là điểm G. B. giao tuyến của (SAB) và (IJG) là SG. C. giao tuyến của (SAB) và (IJG) là đường thẳng MG, với M là giao điểm của đường thẳng qua G và song song với AB với đường thẳng SA. D. giao tuyến của (SAB) và (IJG) là đường thẳng MN, với N là giao điểm của IG với SB, M là giao điểm của JG với...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm khẳng định đúng
A. giao tuyến của (SAB) và (IJG) là điểm G.
B. giao tuyến của (SAB) và (IJG) là SG.
C. giao tuyến của (SAB) và (IJG) là đường thẳng MG, với M là giao điểm của đường thẳng qua G và song song với AB với đường thẳng SA.
D. giao tuyến của (SAB) và (IJG) là đường thẳng MN, với N là giao điểm của IG với SB, M là giao điểm của JG với SA.
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì A. AB 3CD B. AB 2CD C. CD 3AB D. CD 2AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì
A. AB = 3CD
B. AB = 2CD
C. CD = 3AB
D. CD = 2AB
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( đáy lớn AB). Gọi I,J lần lượt là trung điểm của AD và BC, K là điểm trên cạnh SB sao cho SK=2/3SB
a. Tìm giao tuyến của (SAB) và (IJK)
b. Tìm thiết diện của ( IJK) với hình chóp S.ABCD. Tìm điều kiện để thiết diện là hình bình hành
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB và AB 2 CD. Gọi I, J, K lần lượt là ba điểm trên các cạnh SA; AB; BC. Gọi P, Q lần lượt là giao điểm của JK với AD và CD; F là giao điểm của SD và IP. Tìm giao điểm G của SC và mp (IJK) . Tính tỉ số
G
S
G
C
A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB và AB = 2 CD. Gọi I, J, K lần lượt là ba điểm trên các cạnh SA; AB; BC. Gọi P, Q lần lượt là giao điểm của JK với AD và CD; F là giao điểm của SD và IP. Tìm giao điểm G của SC và mp (IJK) . Tính tỉ số G S G C
A. 1
B. 2
C. 3
D. 4