Question

Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm khẳng định đúng

A. giao tuyến của (SAB) và (IJG) là điểm G.

B. giao tuyến của (SAB) và (IJG) là SG.

C. giao tuyến của (SAB) và (IJG) là đường thẳng MG, với M là giao điểm của đường thẳng qua G và song song với AB với đường thẳng SA.

D. giao tuyến của (SAB) và (IJG) là đường thẳng MN, với N là giao điểm của IG với SB, M là giao điểm của JG với SA.

Answer 1

Do IJ là đường trung bình hình thang ABCD nên IJ // AB. Hai mặt phẳng (GIJ) và (SAB) lần lượt chứa hai đường thẳng song song nên giao tuyến của chúng là đường thẳng đi qua G và song song với AB. Đường thẳng này cắt SA tại M và cắt SB tại N.

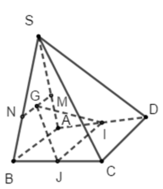
Đáp án C