Các câu hỏi tương tự
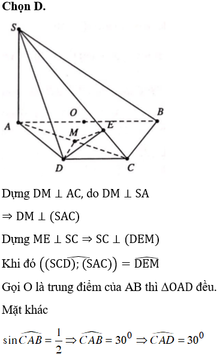
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB 2a.
SA
⊥
(ABCD) và SA
a
3
. Côsin của góc tạo bới hai mặt phẳng (SBC) và (SCD) bằng A.
10
15
B.
10
25
C.
10
10
D. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a. SA ⊥ (ABCD) và SA= a 3 . Côsin của góc tạo bới hai mặt phẳng (SBC) và (SCD) bằng
A. 10 15
B. 10 25
C. 10 10
D. 10 5
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính
A
B
2
a
,
S
A
a
3
và vuông góc với mặt phẳng ABCD. Cosin của góc giữa hai mặt phẳng
S
A
D
và
S
B
C
bằng A.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính A B = 2 a , S A = a 3 và vuông góc với mặt phẳng ABCD. Cosin của góc giữa hai mặt phẳng S A D và S B C bằng
A. 2 2
B. 2 3
C. 2 4
D. 2 5
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính
A
B
2
a
,
S
A
a
3
và vuông góc với mặt phẳng (ABCD) . Tính cosin góc giữa hai mặt phẳng (SAD) và (SBC) bằng: A.
2
2
B.
2
3
C.
2
4...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính A B = 2 a , S A = a 3 và vuông góc với mặt phẳng (ABCD) . Tính cosin góc giữa hai mặt phẳng (SAD) và (SBC) bằng:
A. 2 2
B. 2 3
C. 2 4
D. 2 5
Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường kính AD2a và có cạnh
S
A
⊥
(
A
B
C
D
)
. Tính khoảng cách từ B đến mặt phẳng (SCD) A.
a
2
B.
a
3
C.
a
2
2
D.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường kính AD=2a và có cạnh S A ⊥ ( A B C D ) . Tính khoảng cách từ B đến mặt phẳng (SCD)
A. a 2
B. a 3
C. a 2 2
D. a 3 2
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với AB BC a, AD 2a. Biết SA vuông góc với mặt phằng (ABCD) và
S
A
a
5
.
Côsin của góc tạo bởi hai mặt phẳng (SBC) và (SCD) bằng A.
2
21
21
.
B.
21
12
.
C.
21...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với AB = BC = a,
AD = 2a. Biết SA vuông góc với mặt phằng (ABCD) và S A = a 5 . Côsin của góc tạo bởi hai mặt phẳng (SBC) và (SCD) bằng
A. 2 21 21 .
B. 21 12 .
C. 21 6 .
D. 21 21 .
Cho hình chóp tứ giác S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AD2a,
S
A
⊥
(
A
B
C
D
)
,
S
A
3
2
a
. Tính khoảng cách giữa BD và SC A.
3
a
2
4
B.
a...
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AD=2a, S A ⊥ ( A B C D ) , S A = 3 2 a . Tính khoảng cách giữa BD và SC
A. 3 a 2 4
B. a 2 4
C. 5 a 2 12
D. 5 a 2 4
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB 2a, AD DC a,
S
A
a
2
,
S
A
⊥
(
A
B
C
D
)
.
Tính cosin của góc giữa hai mặt phẳng (SBC) và (SCD). A.
3
3
B.
5
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 2a, AD = DC = a, S A = a 2 , S A ⊥ ( A B C D ) . Tính cosin của góc giữa hai mặt phẳng (SBC) và (SCD).
A. 3 3
B. 5 3
C. 6 3
D. 7 3
Cho hình chóp đều S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AB2a, hai mặt phẳng (SAB),(SAD) vuông góc với mặt phẳng đáy, SB
7
a, M là điểm thỏa mãn
SM
→
2
MD
⇀
. Giá trị cosin góc giữa hai mặt phẳng (MAB) và (MBC) bằng A.
310...
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AB=2a, hai mặt phẳng (SAB),(SAD) vuông góc với mặt phẳng đáy, SB= 7 a, M là điểm thỏa mãn SM → = 2 MD ⇀ . Giá trị cosin góc giữa hai mặt phẳng (MAB) và (MBC) bằng
A. 310 20
B. 3 10 20
C. 11 13 52
D. 5 13 52
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB a. Biết SA a và vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (SCD) bằng
φ
, với
cos
φ
2
5
. Tính theo a thể tích của khối chóp S.ABCD A.
4
3
a
3
B.
2
3
a
3...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a. Biết SA = a và vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (SCD) bằng φ , với cos φ = 2 5 . Tính theo a thể tích của khối chóp S.ABCD
A. 4 3 a 3
B. 2 3 a 3
C. 2 a 3
D. a 3 3