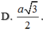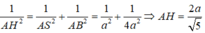
Đáp án D
Ta có mặt cầu S(A;r) tiếp xúc với mặt phẳng (SBC) khi và chỉ khi r = d(A; (SBC)).
Hạ AH ⊥ SB tại H. Do BC ⊥ AB và BC ⊥ SA nên BC ⊥ (SAB) , suy ra BC ⊥ AH.
Mặt khác AH ⊥ SB nên AH ⊥ (SBC) hay d(A; (SBC)) = AH Xét tam giác vuông SAB ta có:
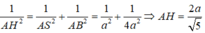
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, SA vuông góc với đáy và SA = 2a. Bán kính mặt cầu tâm A tiếp xúc với SC theo a là:
A. a 3 3
B. 2 a 3 3
C. a 2
D. a 2 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy và SA = 2a. Góc giữa cạnh bên SB và đáy là 45o. Bán kính mặt cầu tâm S và tiếp xúc với BD theo a là:
A. a 6 3
B. a 6 6
C. a 6 2
D. a 6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có đường chéo bằng 2 a, cạnh SA có độ dài bằng 2a và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD?
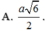
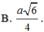
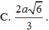
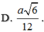
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2AD = 2a. SA vuông góc với đáy, góc giữa cạnh bên SB và đáy là 45o. Bán kính mặt cầu tâm A cắt mặt phẳng (SBD) theo một đường tròn có bán kính bằng a là:
A. a 6 3
B. a 11 2 3
C. a 15 3
D. a 30 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2AD = 2a, SA vuông góc với đáy, SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là:
A. a 3
B. a 6
C. 3 a 3 2
D. a 6 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, cạnh bên SA vuông góc với mặt đáy, SA = a. Gọi H là hình chiếu của a trên SB, tính thể tích khối chóp H.ABCD theo a và côsin của góc giữa 2 mặt phẳng (SBC) và (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính mặt cầu tâm B cắt SC theo một dây có độ dài 2a là:
A. 2 a 2 3
B. 2 a 11 3
C. a 17 3
D. a 10
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
Cho hình chóp S.ABCD có đáy
ABCD là hình vuông cạnh a, SA
vuông góc với mặt đáy và SA=a.
Mặt cầu ngoại tiếp hình chóp
S.ABCD có bán kính bằng
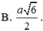
