Chọn đáp án A.
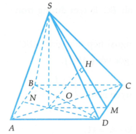
Gọi O là tâm của hình vuông và N là trung điểm của AB.
Khi đó G là giao điểm của AC và DN. Tam giác SGD vuông tại G nên S D G ^ nhọn
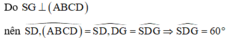
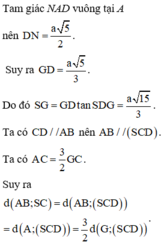

Chọn đáp án A.
Gọi O là tâm của hình vuông và N là trung điểm của AB.
Khi đó G là giao điểm của AC và DN. Tam giác SGD vuông tại G nên S D G ^ nhọn
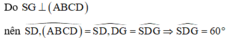
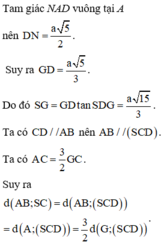


Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABD. Cạnh SD tạo với đáy (ABCD) một góc bằng 60 ° . Khoảng cách từ điểm A tới mặt phẳng (SBC) là
A. 2 a 285 57
B. a 285 57
C. a 285 19
D. 2 a 285 19
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 6a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD,d(G,(SAD))=a (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng SD và BC.
A. 2a
B. 3a
C. 4a
D. 3 2 a
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và A B C ^ = 60 ° . Hình chiếu vuông góc của điểm S lên mặt phẳng A B C D trùng với trọng tâm tam giác ABC. Gọi φ là góc giữa đường thẳng SB với mặt phẳng S C D , tính sin φ biết rằng S B = a .
A. sin φ = 2 2
B. sin φ = 2 3
C. sin φ = 3 2
D. sin φ = 6 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng đáy trùng với trọng tâm tam giác ABD. Cạnh bên SD tạo với đáy một góc 60 0
Tính thể tích khối chóp S.ABCD
A. a 3 15 3
B. a 3 15 27
C. a 3 15 9
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và A B C = 60 ° . Hình chiếu vuông góc của điểm S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABC. Gọi φ là goc giữa đường thẳng SB và mặt phẳng (SCD), tính sin φ biết rằng SB = a.
A. sin φ = 1 4
B. sin φ = 1 2
C. sin φ = 3 2
D. sin φ = 2 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm I thuộc đoạn AB sao cho BI=2AI. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng 60 ° . Tính khoảng cách giữa hai đường thẳng AD và SC.
A. 93 31 a
B. 3 93 31 a
C. 93 31 a
D. 3 93 31 a
Cho hình chóp S.ABCD, có đáy là hình thoi cạnh a, AC=a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Tính khoảng cách giữa hai đường thẳng AD và SC, biết góc giữa SD và mặt đáy bằng 60 °
A. a 906 29
B. a 609 29
C. a 609 19
D. a 600 29
Cho hình chóp S.ABCD có đáy hình chữ nhật, AB = a; AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
A. d = a 1315 89
B. d = 2 a 1315 89
C. d = 2 a 1513 89
D. d = a 1513 89
Cho hình chóp S . A B C D có đáy A B C D là hình thoi cạnh a, góc B A C ⏜ = 60 ° , hình chiếu của đỉnh S trên mặt phẳng A B C D trùng với trọng tâm tam giác A B C , góc tạo bới hai mặt phẳng S A C và A B C D là 60 ° . Khoảng cách từ B đến mặt phẳng S C D theo a bằng
A. 3 a 2 7
B. 9 a 2 7
C. a 2 7
D. 3 a 7