(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ
(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, SA=3a và SA vuông góc với mặt đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) là
A. S A D ^
B. A S D ^
C. S D A ^
D. B S D ^
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Biết SA vuông góc với mặt phẳng đáy và SA = 3a. Thể tích hình chóp S.ABCD là:
A. 6 a 3
B. 12 a 3
C. 2 a 3
D. 1 3 a 3
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết AB = a, AD = 2a, góc giữa cạnh bên SD và mp (ABCD) bằng 60 ° . Tính khoảng cách từ A đến mp (SBD).
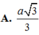
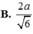
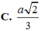
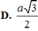
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, AD = 2a. Cạnh bên SA vuông góc với đáy (ABCD), Tính tan của góc giữa hai ămtj phẳng (SBD) và (ABCD)
A . 1 5
B . 2 5
C . 5
D . 5 2
Cho hình chóp S. ABCD đáy ABCD là hình chữ nhật, AB=a, AD=2a. Cạnh bên SA vuông góc với đáy (ABCD), SA=2a. Tính tan của góc giữa hai mặt phẳng (SBD) và (ABCD)
A. 1 5
B. 2 5
C. 5
D. 5 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AD=2a. Cạnh bên SA=2a và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SD
A. a
B. 2a
C. 2 a 5
D. a 2
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a, SA = a 3 vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:
![]()
![]()
![]()
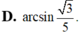
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với mặt phẳng (ABCD), S A = a 3 . Thể tích của khối chóp S.ABC là:
A. 2 a 3 3 3
B. 2 a 3 3
C. a 3 3
D. a 3 3 3