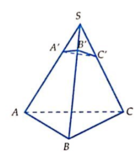
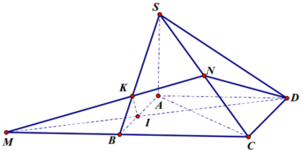
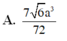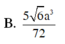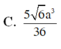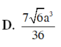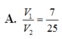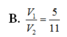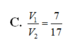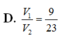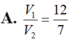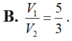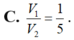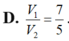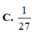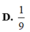Cho hình chóp S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho MA= 2SM, SN = 2NB, là mặt phẳng qua MN và song song với SC. Kí hiệu (H1) và (H2) là các khối đa diện có được khi chia khối chóp S.ABC bới mặt phẳng trong đó (H1) chứa điểm S, (H2) chứa điểm A; V1 và V2 lần lượt là thể tích của (H1) và (H2). Tính tỉ số V 1 V 2
A. 4 3
B. 5 4
C. 3 4
D. 4 5
Chọn D.
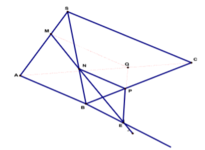
Mp ( α ) qua MN và song song với SC. Mp ( α ) cắt BC và cắt AC tại P và Q ta có:
NP // SC nên ![]() Ta có: MN, PQ, AB đồng quy tại E.
Ta có: MN, PQ, AB đồng quy tại E.
Áp dụng định lí Mennelauyt trong tam giác SAB, ta có:
![]()
![]()
Áp dụng định lí Menelauyt trong tam giác ABC ta có: ![]()
![]()
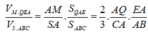
![]()
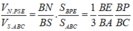
![]()
![]()
![]()
![]()
Vậy