Question

Cho hình chóp S.ABC có SC vuông góc với (ABC) và tam giác ABC vuông tại B. Biết AB=a, AC=a√3​, SC=2a√6. Sin của góc giữa hai mặt phẳng (SAB); (SAC) bằng

Answer 1

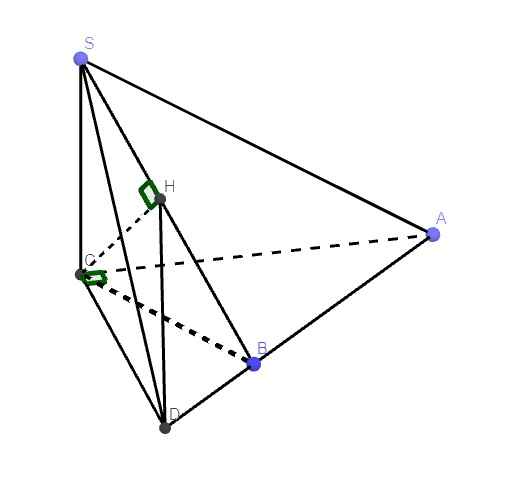
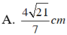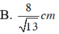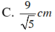Qua C kẻ đường thẳng vuông góc AC cắt AB kéo dài tại D

\(\left\{{}\begin{matrix}SC\perp\left(ABC\right)\Rightarrow SC\perp CD\\CD\perp AC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAC\right)\)

Kẻ \(CH\perp SB\Rightarrow CH\perp\left(SAB\right)\)

\(\Rightarrow\widehat{HCD}\)  là góc giữa (SAB) và (SAC)

\(BC=\sqrt{AC^2-AB^2}=a\sqrt{2}\)

\(\dfrac{1}{CH^2}=\dfrac{1}{SC^2}+\dfrac{1}{BC^2}=\dfrac{13}{24a^2}\Rightarrow CH=\dfrac{2a\sqrt{78}}{13}\)

\(CD=AC.tanA=AC.\dfrac{BC}{AB}=a\sqrt{6}\)

\(sin\widehat{HCD}=\dfrac{DH}{CD}=\dfrac{\sqrt{CD^2-CH^2}}{CD}=...\)

Answer 2