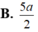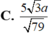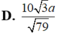Chọn đáp án A
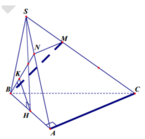
Gọi H là trung điểm của AB suy ra SH ⊥ (ABC)
Trong (SAC) từ M dựng MN // AC , gọi K là hình chiếu của H trên BN
Ta có AC ⊥ (SAB) mà MN //AC ⇒ MN ⊥ (SAB)
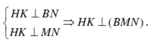
Vì (BMN) // AC suy ra khoảng cách giữa hai đường AC và BM là
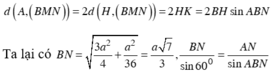

Chọn đáp án A

Gọi H là trung điểm của AB suy ra SH ⊥ (ABC)
Trong (SAC) từ M dựng MN // AC , gọi K là hình chiếu của H trên BN
Ta có AC ⊥ (SAB) mà MN //AC ⇒ MN ⊥ (SAB)
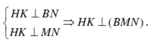
Vì (BMN) // AC suy ra khoảng cách giữa hai đường AC và BM là
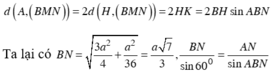

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC = a. Biết SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy (ABC). Tính tang của góc tạo bởi đường thẳng SC và mặt đáy (ABC).
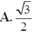
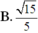
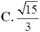

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Tam giác SAC cân tại S có đường cao và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a.
A . a 3 3
B . 2 a 3
C . a 3 2
D . a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC =2a, BC =a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A. a 39 13
B. 3 a 13 13
C. a 39 26
D. a 13 26
Cho hình chóp S.ABC có đấy ABC là tam giác đều cạnh a, SA = SB = SC = 2a. Gọi o là trung điểm AC, G là trọng tâm tam giác ABC a) chứng minh (SGO) vuông góc với (ABC) b) tính góc giữa hai mặt phẳng (SAB) và (ABC) c) tính khoảng cách giữa AB và SC
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a; hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng đáy (ABC). Gọi M là trung điểm của AB; mặt phẳng qua SM và song song với BC cắt AC tại N. Biết góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Khoảng cách giữa hai đường thẳng AB và SN là:
A. 4 a 39 13
B. 3 a 39 13
C. a 39 13
D. 2 a 39 13
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABC). Gọi M là trung điểm của AB, mặt phẳng qua SM song song với BC cắt AC tại N. Biết góc tạo bởi (SBC) và (ABC) là 60 o . Tìm khoảng cách giữa hai đường thẳng AB và SN.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 3HB. Góc giữa đường thẳng SC và mặt phẳng bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a.
A . a 61 4
B . 4 a 17 3
C . a 35 51
D . 4 a 351 3 61
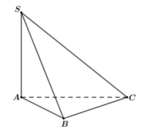
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB =a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 o (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và SC bằng
A. a
B. a 2 2
C. a 3 2
D. a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a và S A ⊥ ( A B C ) . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 o Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
![]()