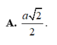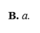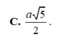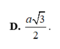Đáp án là C
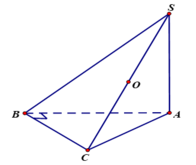
Ta có:
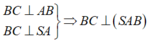
![]()
Do đó 2 điểm A, B nhìn đoạn SC dưới một góc vuông. Suy ra mặt cầu ngoại tiếp hình chóp S. ABC là mặt cầu đường kính SC.
Xét tam giác ABC có
![]()
suy ra
![]()
![]()
Đáp án là C

Ta có:
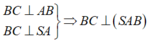
![]()
Do đó 2 điểm A, B nhìn đoạn SC dưới một góc vuông. Suy ra mặt cầu ngoại tiếp hình chóp S. ABC là mặt cầu đường kính SC.
Xét tam giác ABC có
![]()
suy ra
![]()
![]()
Cho hình chóp S.ABC có SA vuông góc mặt phẳng (ABC) tam giác ABC vuông tại B. Biết SA=2a, AB=a, BC=a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho
A. a
B. 2a
C. a 2
D. 2a 2
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
Cho hình chóp S,ABC có SA vuông góc với mặp phẳng (ABC), tam giác ABC vuông tại B. Biết SA=2a, AB=a, BC= a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SA vuông góc với đáy và S A = 2 a . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC.
![]()
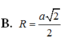
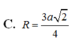
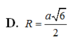
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, biết S A ⊥ ( A B C ) , S A = a , A B = 2 a , A C = 3 a . Tính bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC.
A. r = 13 13 a
B. r = 3 2 a
C. r = a 14
D. r = 14 2 a
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại A có BC = 3 a , SA = 2 a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
![]()

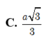
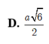
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB = a; SA = SB = a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
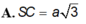
![]()
![]()
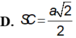
Cho hình chóp S.ABC có đáy ABC là hình vuông tại B và BA=BC=a. Cạnh bên SA=2a và vuông góc với mặt phẳng (ABC). Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
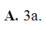
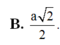
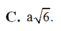
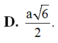
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy và SA = AB = a. Tính bán kính mặt cầu ngoại tiếp khối chóp.