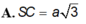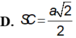Các câu hỏi tương tự
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC) và SASBABACa; SCa
2
. Diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABC bằng: A. 2
πa
2
B.
πa
2
C. 8
πa
2
D. 4
πa
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC) và SA=SB=AB=AC=a; SC=a 2 . Diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABC bằng:
A. 2 πa 2
B. πa 2
C. 8 πa 2
D. 4 πa 2
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với ABACa cạnh SASBa và có
S
B
C
⊥
A
B
C
. Tính SC để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng a. A.
S
C
a
B.
S
C
a
2
C.
S
C
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB=AC=a cạnh SA=SB=a và có S B C ⊥ A B C . Tính SC để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng a.
A. S C = a
B. S C = a 2
C. S C = a 3
D. S C = 2 a
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với ABACa, cạnh SASBa và có (SBC)
⊥
(ABC). Tính SC để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng a.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB=AC=a, cạnh SA=SB=a và có (SBC) ⊥ (ABC). Tính SC để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng a.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với ABACa. Cạnh bên SASBa và có
S
B
C
⊥
A
B
C
. Tính độ dài SC để bán kính mặt cầu ngoại tiếp hình chóp bằng a A.
S
C
a
B.
S
C
a
2
C.
S
C
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với AB=AC=a. Cạnh bên SA=SB=a và có S B C ⊥ A B C . Tính độ dài SC để bán kính mặt cầu ngoại tiếp hình chóp bằng a
A. S C = a
B. S C = a 2
C. S C = a 3
D. S C = 2 a
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, ABBCa và
∠
A
B
C
120
°
. Cạnh bên SA vuông góc với mặt phẳng đáy và SA2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC. A.
a
2
5
B. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tại với mặt phẳng (ABC) một góc là 60o. Bán kính mặt cầu ngoại tiếp hình chóp là: A. a
3
B. a
2
C. a
3
/2 D. a
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC = a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tại với mặt phẳng (ABC) một góc là 60o. Bán kính mặt cầu ngoại tiếp hình chóp là:
A. a 3
B. a 2
C. a 3 /2
D. a
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại A có BC
3
a
, SA
2
a
và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
Đọc tiếp
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại A có BC = 3 a , SA = 2 a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
![]()

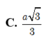
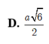
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A và AB SB a, SB vuông góc với mặt phẳng (ABC). Bán kính nhỏ nhất của mặt cầu tiếp xúc với đường thẳng SC và AB là: A. a B.
a
2
2
C.
a
2
4
D.
a
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A và AB = SB = a, SB vuông góc với mặt phẳng (ABC). Bán kính nhỏ nhất của mặt cầu tiếp xúc với đường thẳng SC và AB là:
A. a
B. a 2 2
C. a 2 4
D. a 2
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA2a, ABa, BCa
3
. Tính bán kính R của mặt cầu ngoại tiếp hình chóp. A.
a
. B.
2
2
a
. C.
2
a
. D.
3
a...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA=2a, AB=a, BC=a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp.
A. a .
B. 2 2 a .
C. 2 a .
D. 3 a .