Đáp án A
Do S A ⊥ ( A B C ) nên B C ⊥ S A M là trung điểm BC nên ta có B C ⊥ A M
⇒ B C ⊥ ( S A M ) độ dài cạnh hình lập phương là 3cm
Đáp án A
Do S A ⊥ ( A B C ) nên B C ⊥ S A M là trung điểm BC nên ta có B C ⊥ A M
⇒ B C ⊥ ( S A M ) độ dài cạnh hình lập phương là 3cm
Cho hình chóp SABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, M là trung điểm BC, J là hình chiếu của A lên BC. Khẳng định nào sau đây đúng ?
A. BC ⊥ (SAC)
B.BC ⊥ (SAM)
C.BC ⊥ (SAJ)
D. BC ⊥ (SAB)
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, cạnh bên SA vuông góc với đáy, M là trung điểm của BC, J là trung điểm của BM. Mệnh đề nào sau đây đúng?
A. BC ⊥ (SAC).
B. BC ⊥ (SAJ).
C. BC ⊥ (SAM).
D. BC ⊥ (SAB).
Hình chóp A'.BC'D có đáy ABC là tam giác vuông tại a, SA vuông góc với mặt phẳng (ABC), SA = a, AB = b, AC = c. Tính bán kính R của mặt cầu đi qua các điểm A, B, C và S ?
A. R = 2 ( a + b + c ) 3
B. R = 2 a 2 + b 2 + c 2
C. R = 1 2 a 2 + b 2 + c 2
D. R = a 2 + b 2 + c 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC = 2a,BC = a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60 o . Tính theo a thể tích V của khối chóp S.ABC?
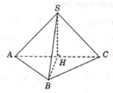
A. V = a 6 3 4 .
B. V = a 6 3 6 .
C. V = a 3 2 .
D. V = a 6 3 12 .
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, A B C ^ = 60 ° . Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm M của BC, góc giữa SA và mặt đáy bằng 450. Thể tích của khối chóp SABC bằng
![]()
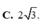
![]()
Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SC hợp với đáy một góc 300, M là trung điểm của AC. Tính thể tích khối chóp S. BCM.
A. 3 a 3 48
B. 3 a 3 16
C. 3 a 3 96
D. 3 a 3 24
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh AB=2, A B C ⏜ = 60 0 . Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm M của BC, góc giữa SA và mặt đáy bằng 45 0 . Tính thể tích V của khối chóp SABC.
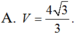

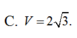
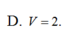
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết SA ⊥ (ABCD), AB=BC=a, SA=a 2 , AD=2a. Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm S, A, B, C, E.
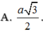
![]()
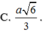
![]()