Đáp án B
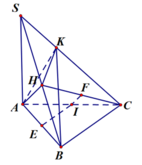
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC.
IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB. Suy ra bán kính R = a 2 2
Đáp án B

Gọi I, E, F lần lượt là trung điểm của AC, AB, HC.
IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB. Suy ra bán kính R = a 2 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Tính thể tích khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKB là
A. π a 3 2
B. 2 π a 3 3
C. 2 π a 3
D. π a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a. Cạnh bên SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB và SC. Tính thể tích của khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKB.
A. 2 π a 3 .
B. π a 3 6 .
C. π a 3 2 .
D. 2 π a 3 3 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Thể tích của khối cầu ngoại tiếp chóp A.HKCB bằng
A. 2 π a 3
B. π a 3 2
C. 2 π a 3 3
D. π a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a. Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN
A. V = a 3 36
B. V = a 3 5 15
C. V = a 3 3 18
D. V = a 3 30
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B , AB = a . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 0 . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
A. 8 2 πa 3 3
B. 4 2 πa 3 3
C. 2 2 πa 3 3
D. 2 πa 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A, B, C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A,B,C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B, A B = d . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 ° . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu .
A. 4 2 πa 3 3
B. 2 2 πa 3 3
C. 8 2 πa 3 3
D. 2 πa 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính theo a bán kính R của mặt cầu đi qua năm điểm A , B , C , B 1 , C 1
A. R = a 3 6
B. R = a 3 2
C. R = a 3 6
D. R = a 3 6