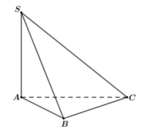
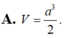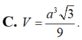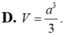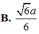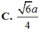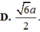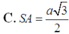Trong mp(ABC), Kẻ AK⊥BC tại K
Trong mp(SAK), kẻ AH⊥SK tại H
Ta có: BC⊥AK
BC⊥SA(SA⊥(ABC))
SA,AK cùng thuộc mp(SAK)
Do đó: BC⊥(SAK)
=>BC⊥AH
Ta có: AH⊥SK
AH⊥BC
mà SK,BC cùng thuộc mp(SBC)
nên AH⊥(SBC)
=>KHoảng cách từ A đến mp(SBC) là AH
Xét ΔSAK vuông tại A có AH là đường cao
nên \(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AK^2}\)
=>\(\frac{1}{AK^2}=\frac{1}{AH^2}-\frac{1}{SA^2}=\frac{1}{\left(\frac{a\sqrt{21}}{7}\right)^2}-\frac{1}{a^2}=\frac{1}{a^2\cdot\frac{21}{49}}-\frac{1}{a^2}=\frac{1}{\frac{3a^2}{7}}-\frac{1}{a^2}\)
\(=\frac{7}{3a^2}-\frac{3}{3a^2}=\frac{4}{3a^2}\)
=>\(AK^2=\frac{3a^2}{4}\)
=>\(AK=\frac{a\sqrt3}{2}\)
ΔABC cân tại A
mà AK là đường cao
nên K là trung điểm của BC
ΔABC vuông tại A
mà AK là đường trung tuyến
nên \(BC=2\cdot AK=a\sqrt3\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(2\cdot AB^2=\left(a\sqrt3\right)^2=3a^2\)
=>\(AB^2=\frac{3a^2}{2}=\frac{6a^2}{4}\)
=>\(AB=\frac{a\sqrt6}{2}\)
=>\(AC=AB=\frac{a\sqrt6}{2}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\frac12\cdot AB\cdot AC=\frac12\cdot\frac{a\sqrt6}{2}\cdot\frac{a\sqrt6}{2}=\frac{a^2\cdot6}{8}=a^2\cdot\frac34\)
Thể tích hình chóp S.ABC là:
\(V_{S.ABC}=\frac13\cdot SA\cdot S_{ABC}=\frac13\cdot a\cdot a^2\cdot\frac34=\frac14a^3=\frac14\cdot\left(\sqrt3\right)^3=\frac{3\sqrt3}{4}\)