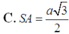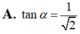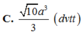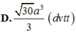Question

cho hình chóp s abcd có đáy abcd là hình vuông cạnh 2a, các mặt phẳng (SAB) và (SAD) vuông góc với đáy tính thể tích khối chóp s.ABCD trong các trường hợp sau: a/ SA=3cm b/góc nửa mặt bên (SCD) và mặt đáy bằng 60

Answer 1

a: (SAB)⊥(ABCD)

(SAD)⊥(ABCD)

(SAD) cắt (SAB) tại SA

Do đó: SA⊥(ABCD)

Diện tích đáy là \(S=2a\cdot2a=4a^2\)

Thể tích là \(V=\frac13\cdot SA\cdot S_{ABCD}=\frac13\cdot3\cdot4a^2=4a^2\)

b: Ta có: CD⊥AD(ABCD là hình vuông)

CD⊥SA(SA⊥(ABCD))

AD,SA cùng thuộc mp(SAD)

Do đó: CD⊥(SAD)

=>CD⊥SD

Ta có: (SCD) cắt (ABCD) tại CD

(SCD) có CD⊥SD

(ABCD) có AD⊥SD

Do đó: \(\hat{\left(SCD\right)};\left(ABCD\right)=\hat{SD;DA}=\hat{SDA}=60^0\)

Xét ΔSAD vuông tại A có \(tanSDA=\frac{SA}{AD}\)

=>\(SA=AD\cdot\tan60=2a\cdot\tan60=2\sqrt3\cdot a\)

=>\(V_{S.ABCD}=\frac13\cdot SA\cdot S_{ABCD}=\frac13\cdot a\cdot2\sqrt3\cdot4a^2=8\sqrt3\cdot\frac{a^3}{3}\)