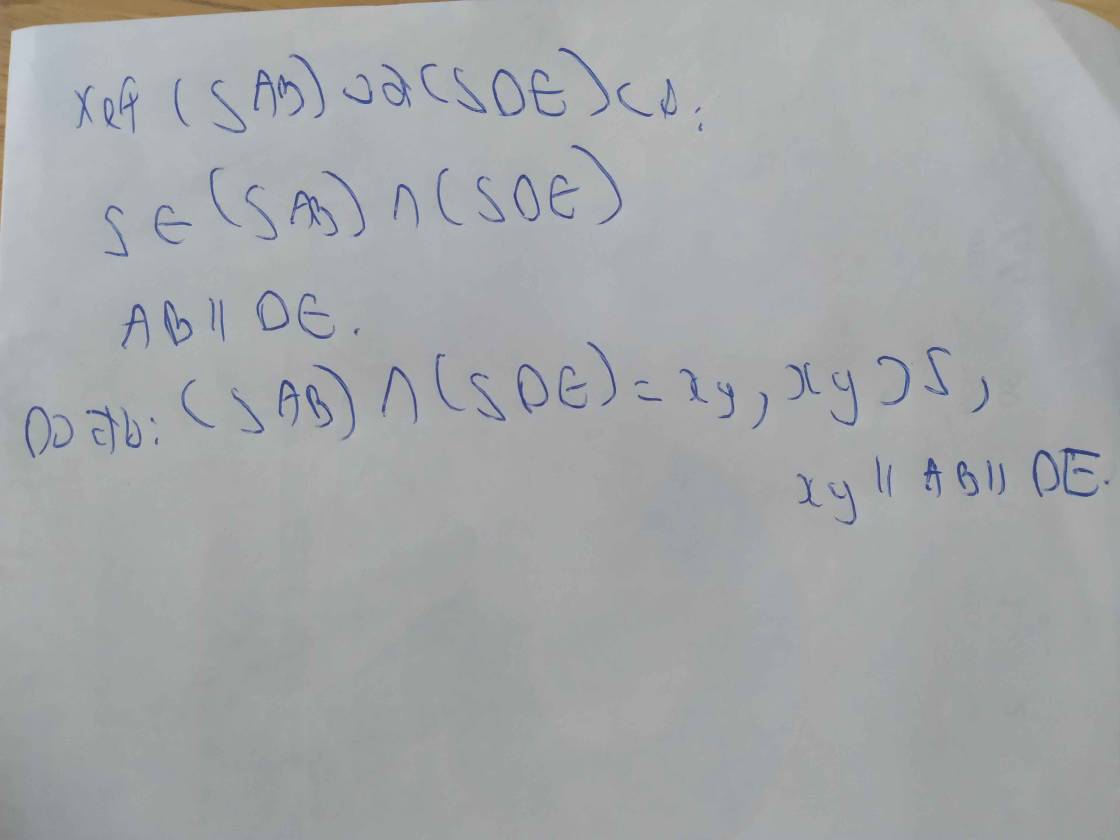Các câu hỏi tương tự
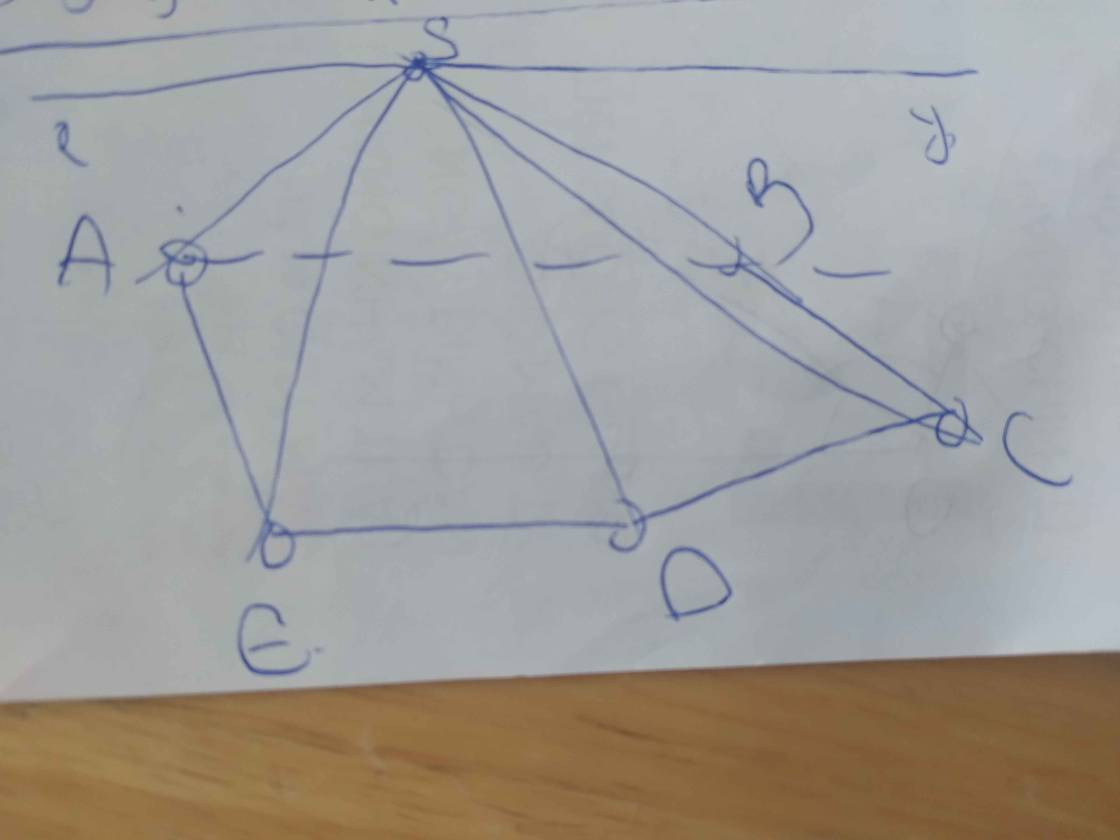
Cho hình chóp ngũ giác S.ABCDE. Giả sử AB song song với DE. b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SDE).
Cho hình chóp ngũ giác S.ABCDE. Giả sử AB song song với DE. b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SDE).
cho hình chóp S.ABCD đáy ABCD là tứ giác lồi (các cặp cạnh đối không song song. Gọi F là điểm thuộc cạnh SB
a) tìm giao tuyến của 2 mặt phẳng (SAB) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SDF)
c) tìm giao tuyến của 2 mặt phẳng (FCD) và (SBC)
Cho hình chóp S.ABCD có đáy ABCD là tứ giác có các cặp cạnh đối không song song với nhau a) tìm giao điểm của đường thẳng SA và mặt phẳng (ABCD) b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I,J lần lượt là trung điểm của AB và BC. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với:
A. BJ
B. AD
C. BI
D. IJ
cho hình chóp S.ABCD đáy ABCD là tứ giác lồi (các cặp cạnh đối không song song. Gọi E là điểm thuộc cạnh SC
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
Cho hình chóp S.ABCD có các cạnh AB và CD không song song ; O là giao điểm của hai đường thẳng AC và BD. Giao tuyến của các cặp mặt phẳng (SAC) và (SBD), (SAB) và (SCD) lần lượt là:
A. SA và SI, I là giao điểm của AB, CD
B. SO và SI, I là giao điểm của AB, CD
C. SB và SO
D. SD và SO
Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD . Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và SC. Thiết diện đó là hình gì?
Cho hình chóp S.ABCD đáy ABCD là hình bình hành, tâm O. K là trung đểm của SA. Xác định vị trí của H trên AC để thiết diện của hình chóp S.ABCD với mặt phẳng (∝) chứa KH và song song với BD là ngũ giác. A. H thuộc đoạn OC và khác O, C B. H thuộc đoạn OA và khác O, A C. H thuộc đoạn AC và khác A, C D. H thuộc đoạn AC và khác A, C
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình bình hành, tâm O. K là trung đểm của SA. Xác định vị trí của H trên AC để thiết diện của hình chóp S.ABCD với mặt phẳng (∝) chứa KH và song song với BD là ngũ giác.
A. H thuộc đoạn OC và khác O, C
B. H thuộc đoạn OA và khác O, A
C. H thuộc đoạn AC và khác A, C
D. H thuộc đoạn AC và khác A, C