Đáp án C
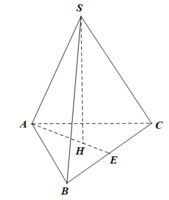
A E ⊥ B C S E ⊥ B C ⇒ S B C ; A B C = S E ; A E = ∠ S E A = 60 0 H E = 1 3 . a 3 2 = a 3 6 S H = H E . tan S E A = a 3 6 . 3 = a 2
Đáp án C

A E ⊥ B C S E ⊥ B C ⇒ S B C ; A B C = S E ; A E = ∠ S E A = 60 0 H E = 1 3 . a 3 2 = a 3 6 S H = H E . tan S E A = a 3 6 . 3 = a 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = 2 a , B C = a . Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 60 ° Tính góc giữa hai đường thẳng SB và AC.
A. 60 °
B. 19 ° 45 ' 31 , 78 ' '
C. 70 ° 14 ' 28 , 22 ' '
D. 57 ° 41 ' 18 , 48 ' '
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 o . Tính thể tích khối chóp S.ABCD.
A. a 3 3
B. a 42 12
C. a 42 8
D. a 3 12
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH = a, CH= 3 a. Tính khoảng cách giữa hai đường thẳng SD và CH
A. 2 15 a 3
B. 2 18 a 3
C. 2 22 a 11
D. 14 a 2
Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính diện tích S của mặt cầu ngoại tiếp hình chóp đã cho.
A. S = 16 πa 2 9
B. S = 64 πa 2 9
C. S = 16 πa 2 3
D. S = 64 πa 2 3
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA=2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho H A = 2 H B . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a, gọi I là trung điểm của AB, hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của CI, góc giữa SA và mặt đáy bằng 45 ° (tham khảo hình vẽ bên dưới). Khoảng cách giữa 2 đường thẳng SA và CI bằng:
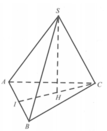
A. a 21 14
B. a 77 22
C. a 14 8
D. a 21 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 60 ° . Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 15 6
B. V = a 3 3 6
C. V = a 3 3 3
D. V = a 3 15 3
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 3HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a.
A. a 61 4
B. 4 a 17 3
C. 4 a 35 51
D. 4 a 351 3 61