Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: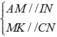
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
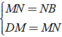 ⇒ DM = MN = NB
⇒ DM = MN = NB

Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: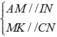
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
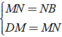 ⇒ DM = MN = NB
⇒ DM = MN = NB
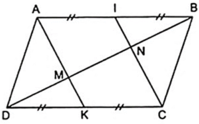
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng: AK//CI
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AB và CD. Nối AF và CE, 2 đường này cắt đường chéo BD lần lượt tại M và N. Chứng minh vectơ DM = vectơ MN = vectơ NB.
hình bình hành ABCD, I,K lần lượt là trung điểm CD, AB, đường chéo BD cắt AI, Ck tại M,N.
CMR:
a, AI//CK
b, DM=MN=NB
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
Cho hình bình hành ABCD, E và F lần lượt là trung điểm của AB, CD. Gọi M, N lần lượt là giao điểm của AF, CE VỚI BD.
a) Chứng minh: Tứ giác AECF là hình bình hành
b) Chứng minh DM = MN = NB
c) Chứng minh MENF là hình bình hành.
d) AN cắt BC tại I. Chứng minh IJ,MN, EF đồng quy.
Bài 3. Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của các cạnh AB và CD, M và N là giao điểm của đường thẳng AI và đường thẳng CK với đường thẳng BD.
a) Chứng minh: AI // CK .
b) Chứng minh: DM = MN = NB
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm AB và CD. Gọi M, N lần lượt là giao điểm của AF và CE với đường chéo DB. Chứng minh:
a/ DM = MN = NB
b/ EMFN là hình bình hành.
c/ Gọi I, J lần lượt là trung điểm của BC và AD. Chứng minh IJ, MN, EF đồng quy.
Giúp mình với
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB và CD, M và N là giao điểm của AI và CK với BD
a) Chứng minh : AI song song với CK
b) Chứng minh DM=MN=NB
Cho hình bình hành ABCD . Gọi M,N lần lượt là trung điểm của AB và CD. Đường chéo BD cắt AN, CM theo thứ tự ở E và K. Chứng minh AK đi qua trung điểm của I của AB.