Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
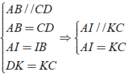
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.

Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
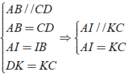
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng: DM = MN = NB
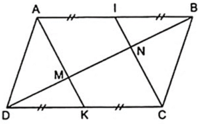
Cho hình bình hành ABCD . Gọi M,N lần lượt là trung điểm của AB và CD. Đường chéo BD cắt AN, CM theo thứ tự ở E và K. Chứng minh AK đi qua trung điểm của I của AB.
Cho hình bình hành ABCD. gọi M,N lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AN, CM theo thứ tự ở E và K. Chứng minh AK đi qua trung điểm của I của BC.
Cho hình bình hành ABCD. gọi M,N lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AN, CM theo thứ tự ở E và K. Chứng minh AK đi qua trung điểm của I của BC.
Cho hình bình hành ABCD. Gọi M,N lần lượt là trung điểm của AB,CD. Đường chéo BD cắt AN,CM theo thứ tự ở E và K. Chứng minh:
a) AMCN là hình bình hành
b) DE=KB
c) AK đi qua trung điểm I của BC
hộ mình ạ
cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AN, CM theo thứ tự ở E và K. Chứng minh:
a) AMCN là hình bình hành
b) DE=KB
c) AK đi qua trung điểm I của BC
Cho hình bình hành ABCD,gọi I,K lần lượt là trung điểm của CD,AB. Đường chéo BD cắt CK và CA lần lượt tại M và O
a, chứng minh AKCI là hình bình hành
b, K,O,I thẳng hàng
c, AM cắt BC tại E. Tính tỉ số EI/BD
Cho hình bình hành ABCD. Gọi E, K lần lượt là trung điểm của CD và AB. Đường chéo BD cắt AE, AC, CK lần lượt tại N, O, M
a) Chứng minh AECK là hình bình hành
b) Chứng minh ba điểm O, E, K thẳng hàng
c) Chứng minh DN = NM = MB
d) Chứng minh AE = 3KM
Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB, CD. Đường chéo BD cắt CM tại E
a)Chứng minh tứ giác AMCN là hình bình hành.
b)Gọi I là giao điểm của AC và BD, chứng minh ba điểm M, N, I thẳng hàng và BI = 3FI