Các câu hỏi tương tự
Cho hình chữ nhật ABCD (AD AB) . Hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng vuông góc với BD cắt tia BC tại E .a) Chứng minh tam giác BDE đồng dạng với tam giácDCE .b) Kẻ CH vuông góc với DE tại H . Chứng minh rằng: 2 . DC CH DB . Từ đó tínhđộ dài CH biết AD 6cm ; AB 8cm.c) Gọi K là giao điểm của OE và HC . Chứng minh:HK /ODEK/EO, từ đó suy ra: K là trung điểm của HC .d) Chứng minh ba đường thẳng ,, OE. CD .BH đồng quy
Đọc tiếp
Cho hình chữ nhật ABCD (AD <AB) . Hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng vuông góc với BD cắt tia BC tại E .
a) Chứng minh tam giác BDE đồng dạng với tam giácDCE .
b) Kẻ CH vuông góc với DE tại H . Chứng minh rằng: 2 . DC CH DB = . Từ đó tính
độ dài CH biết AD = 6cm ; AB = 8cm.
c) Gọi K là giao điểm của OE và HC . Chứng minh:
HK /OD=EK/EO, từ đó suy ra: K là trung điểm của HC .
d) Chứng minh ba đường thẳng ,, OE. CD .BH đồng quy
Cho hình bình hành ABCD có Â 900 , hai đường chéo AC cắt BD tại M. Lấy điểm N đối xứng với C qua D.1)Chứng minh tứ giác ABDN là hình bình hành2)Gọi P là giao điểm của AD và BN. Chứng minh DC 2PM3)Kẻ AH vuông góc với DC tại Ha)Chứng minh : HP PDb)Lấy điểm E là điểm đối xứng với P qua DC. Chứng minh tứ giác HPDE là hình thoi.4)Tia ED cắt đường thẳng AB tại K. Chứng minh DB CK
Đọc tiếp
Cho hình bình hành ABCD có Â > 900 , hai đường chéo AC cắt BD tại M. Lấy điểm N đối xứng với C qua D.
1)Chứng minh tứ giác ABDN là hình bình hành
2)Gọi P là giao điểm của AD và BN. Chứng minh DC = 2PM
3)Kẻ AH vuông góc với DC tại H
a)Chứng minh : HP = PD
b)Lấy điểm E là điểm đối xứng với P qua DC. Chứng minh tứ giác HPDE là hình thoi.
4)Tia ED cắt đường thẳng AB tại K. Chứng minh DB = CK
Cho hình chữ nhật ABCD, kẻ AH vuông góc với đường chéo BDa) Chứng minh ΔAHD và ΔDCB đồng dạng và
B
C
2
D
H
.
D
B
b) Gọi S là trung điểm của BH, R là trung điểm của AH.Chứng minh SH.BD SR.DCc) Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hànhd) Tính góc AST
Đọc tiếp
Cho hình chữ nhật ABCD, kẻ AH vuông góc với đường chéo BD
a) Chứng minh ΔAHD và ΔDCB đồng dạng và B C 2 = D H . D B
b) Gọi S là trung điểm của BH, R là trung điểm của AH.
Chứng minh SH.BD = SR.DC
c) Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hành
d) Tính góc AST
Hình bình hành ABCD có hai đường chéo AC,BD cắt nhau tại O và AC=2.AB. Lấy E là trung điểm AO, M là trung điểm BC
a)Chứng minh tam giác ABE đồng dạng với tam giác ACB
b)Chứng minh EM vuông góc với BD
Cho hình chữ nhật ABCD có AD 6 cm , AB 8 cm , hai đường chéo AC và BD cắt nhau tại O , Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại Ea) Chứng minh rằng tam giác BDE đồng dạng với tam giác DCEb) Kẻ CH vuông góc CE tại H , chứng minh rằng : DC^2 CH * DBc) Gọi K là giao điểm của OE và HC . Chứng minh rằng K là trung điểm của HC , và tính tỉ số diện tích của tam giác EHC và tam giác EDBd) Chứng minh rằng ba đường thẳng OE , CD , BH đồng quy
Đọc tiếp
Cho hình chữ nhật ABCD có AD = 6 cm , AB = 8 cm , hai đường chéo AC và BD cắt nhau tại O , Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại E
a) Chứng minh rằng tam giác BDE đồng dạng với tam giác DCE
b) Kẻ CH vuông góc CE tại H , chứng minh rằng : DC^2 = CH * DB
c) Gọi K là giao điểm của OE và HC . Chứng minh rằng K là trung điểm của HC , và tính tỉ số diện tích của tam giác EHC và tam giác EDB
d) Chứng minh rằng ba đường thẳng OE , CD , BH đồng quy
Cho hình chữ nhật ABCD có AD 6 cm , AB 8 cm , hai đường chéo AC và BD cắt nhau tại O , Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại Ea) Chứng minh rằng tam giác BDE đồng dạng với tam giác DCEb) Kẻ CH vuông góc CE tại H , chứng minh rằng : DC^2 CH * DBc) Gọi K là giao điểm của OE và HC . Chứng minh rằng K là trung điểm của HC , và tính tỉ số diện tích của tam giác EHC và tam giác EDBd) Chứng minh rằng ba đường thẳng OE , CD , BH đồng quy
Đọc tiếp
Cho hình chữ nhật ABCD có AD = 6 cm , AB = 8 cm , hai đường chéo AC và BD cắt nhau tại O , Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại E
a) Chứng minh rằng tam giác BDE đồng dạng với tam giác DCE
b) Kẻ CH vuông góc CE tại H , chứng minh rằng : DC^2 = CH * DB
c) Gọi K là giao điểm của OE và HC . Chứng minh rằng K là trung điểm của HC , và tính tỉ số diện tích của tam giác EHC và tam giác EDB
d) Chứng minh rằng ba đường thẳng OE , CD , BH đồng quy
Bài 4. Cho hình bình hành ABCD có Â 90 độ , hai đường chéo AC cắt BD tại M. Lấy điểm N đối xứng với C qua D.1) Chứng minh tứ giác ABDN là hình bình hành2) Gọi P là giao điểm của AD và BN. Chứng minh DC 2PM3) Kẻ AH vuông góc với DC tại Ha) Chứng minh : HP PDb) Lấy điểm E là điểm đối xứng với P qua DC. Chứng minh tứ giác HDPE là hình thoi.4) Tia ED cắt đường thẳng AB tại K. Chứng minh DB CK
Đọc tiếp
Bài 4. Cho hình bình hành ABCD có Â > 90 độ , hai đường chéo AC cắt BD tại M. Lấy điểm N đối xứng với C qua D.
1) Chứng minh tứ giác ABDN là hình bình hành
2) Gọi P là giao điểm của AD và BN. Chứng minh DC = 2PM
3) Kẻ AH vuông góc với DC tại H
a) Chứng minh : HP = PD
b) Lấy điểm E là điểm đối xứng với P qua DC. Chứng minh tứ giác HDPE là hình thoi.
4) Tia ED cắt đường thẳng AB tại K. Chứng minh DB = CK
Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB. Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD.
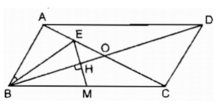
Cho hình bình hành ABCD có AC > BD . Gọi giao điểm hai đường chéo là O. Qua C kẻ CE vuông góc với AB và CG vuông góc với AD. Chứng minh : OA .OD = OC .OB
Tam giác BCE đồng dạng với tam giác DCG









