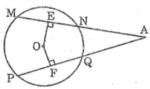
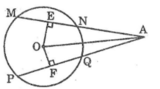
Nối OA
Ta có: MN = PQ (gt)
Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OAE và OAF, ta có:
OA chung
OE = OF (chứng minh trên)
Suy ra: ΔOAE = ΔOAF (cạnh huyền, cạnh góc vuông)
Suy ra: AE = AF
Cho hình bên, trong đó MN = PQ. Chứng minh rằng: AN = AQ
Cho hình vẽ sau, trong đó MN=PQ. Chứng minh rằng:
a, AE=AF
b, AN=AQ.
Cho tam giác ABC gọi P là trung điểm của BC; AE và AF thứ tự là đường phân giác trong và ngoài của góc A; H là hình chiếu A lên BC chứng minh rằng EF.DH=AB.AC
Cho hình vuông ABCD. Lấy điểm E trên cạnh BC. Tia AE cắt đường thẳng CD tại G. Trên mặt phẳng bờ là đg thẳng AE chứa tia AD, kẻ AF vuông góc AE và AF= AE.
b. chứng minh \(\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AG^2} \)
a. chứng minh F, D, C thẳng hàng
c. Biết AD= 13cm, AF : AG= 1:3. Tính độ dài của FG
Cho hình chữ nhật ABCD,AB=2BC,E thuộc BC.Tia AE giao CD tại F,Chứng minh rằng \(\frac{1}{\left(AB\right)^2}=\frac{1}{\left(AE\right)^2}+\frac{1}{4\left(AF\right)^2}\)
Cho đường tròn đường kính AB, d tiếp xúc (O) tại A. Dựng đường kính MN khác AB, các đường thẳng BM, BN cắt d tại E, F
a,Chứng minh AMBN là hình chữ nhật
b,Chứng minh MN tiếp xúc với đường tròn đường kính AE, AF
c, Chứng minh AE.AF ko đổi
d, Tìm vị trí MN để EF min ,diện tích MENF min , ME + NF nhỏ nhất
cho hình vuông ABCD,E thuộc BC qua A kẻ tia Ax vuông góc AE cắt CD tại F.trung tuyết Ay của tam giác AEF cắt CD ở K a,chứng minh rằng AF^2 = FK . FC b,chứng minh rằng khi E di chuyển trên cạnh BC thì chu vi tam giác EKC có giá trị không đổi
cho hình vuông ABCD,E thuộc BC qua A kẻ tia Ax vuông góc AE cắt CD tại F.trung tuyết Ay của tam giác AEF cắt CD ở K a,chứng minh rằng AF^2 = FK . FC b,chứng minh rằng khi E di chuyển trên cạnh BC thì chu vi tam giác EKC có giá trị không đổi
Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH
b) Gọi E, F lần lượt là hình chiếu của H lên AB, AC.
Chứng minh rằng: AE. AB = AF. AC
