Các câu hỏi tương tự
cho hàm số yfleft(xright) liên tục trên R thỏa limlimits_{xrightarrow-infty}fleft(xright)+infty , limlimits_{xrightarrow+infty}fleft(xright)-dfrac{1}{2}tìm số đường tiệm cận củ đồ thị hàm số đã cholimlimits_{xrightarrow-infty}fleft(xright)+infty
Đọc tiếp
cho hàm số \(y=f\left(x\right)\) liên tục trên R thỏa
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\) , \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\dfrac{1}{2}\)
tìm số đường tiệm cận củ đồ thị hàm số đã cho
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\)
#HELP
Hình bên là đồ thị của một hàm số y=f(x) y=f(x) , f(x) f(x) không xác định tại x = -1 x=−1 . Dự đoán \lim\limits_{x\rightarrow-1}f\left(x\right) x→−1 lim f(x) .
#THANKS _YOU
tìm m thỏa mãn yêu cầu bài toána) đồ thị hàm số ydfrac{mx-1}{2x+m} có đường tiệm cận đứng đi qua điểm A (-1;sqrt{2})b) đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số ydfrac{x-2}{2x-m}c) biết đồ thị hàm số ydfrac{left(m+1right)x+2}{x-n+1} nhận trục hoành và trục tung làm 2 đường tiệm cận. Tính m+nd) đồ thị hàm số ydfrac{x-1}{x^2+2left(m-1right)x+m^2-2} có 2 đường tiệm cận đứng
Đọc tiếp
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\) có đường tiệm cận đứng đi qua điểm A (-1;\(\sqrt{2}\))
b) đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
c) biết đồ thị hàm số \(y=\dfrac{\left(m+1\right)x+2}{x-n+1}\) nhận trục hoành và trục tung làm 2 đường tiệm cận. Tính m+n
d) đồ thị hàm số \(y=\dfrac{x-1}{x^2+2\left(m-1\right)x+m^2-2}\) có 2 đường tiệm cận đứng
Cho hàm số y f(x) liên tục trên
ℝ
{1} và có bảng biến thiên như sau: Đồ thị hàm số
y
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng? A. 1 B. 2 C. 0 D. 2
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ \{1} và có bảng biến thiên như sau:
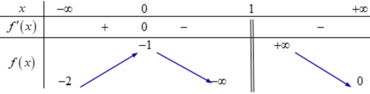 Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
A. 1
B. 2
C. 0
D. 2
xác định đường tiệm cận ngang của đồ thị hàm số sau
a) \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
b) \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\) có đường tiệm cận ngang đi qua điểm A (-1;3)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = -2
Cho hàm số yf(x) và yg(x) là hai hàm liên tục trên
ℝ
có đồ thị hàm số y f (x) là đường cong nét đậm và y g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của yf (x) và yg(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) f(x) - g(x) trên đoạn [a;c]?
Đọc tiếp
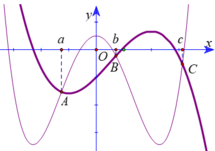
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
![]()
![]()
![]()
![]()
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\) có đường tiệm cận ngang đi qua điểm M (-2;1)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = 1
Cho hàm số
f
x
x
2
n
ế
u
x
≥
0
x
2
...
Đọc tiếp
Cho hàm số f x = x 2 n ế u x ≥ 0 x 2 - 1 n ế u x < 0
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0
b) Dùng định nghĩa chứng minh định nghĩa trên