
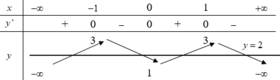
Vậy phương trình (*) có 4 nghiệm phân biệt


Vậy phương trình (*) có 4 nghiệm phân biệt
Cho hàm số y=f(x) xác định và liên tục trên ℝ và có bảng biến thiên như sau:
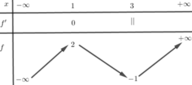
Số nghiệm của phương trình f(x)-3=0 là
A. 3.
B. 0.
C. 1.
D. 2.
Cho hàm số y = f(x) liên tục trên có bảng biến thiên như sau:

Biết f(0)<0, phương trình f(|x|)=f(0) có bao nhiêu nghiệm?
A. 4
B. 5
C. 3
D. 2
Cho hàm số y=f(x) xác định, liên tục trên ℝ có bảng biến thiên như hình vẽ bên. Tìm số nghiệm của phương trình 3|f(x)|-7=0

A. 4
B. 5
C. 6
D. 0
Cho hàm số y = f(X) xác định trên R\{-1} , liên tục trên từng khoảng xác định và có bảng biến thiên như hình dưới đây.
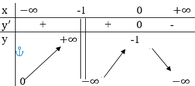
Số nghiệm của phương trình [ f ( x ) ] 2 + f ( x ) + x x = 1 là
A. 1.
B. 0.
C. 2.
D. 3.
Cho hàm số y=f(x) xác định trên R / 2 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
Tìm tập hợp các giá trị của tham số m để phương trình 2f(x)-m=0 có hai nghiệm.
A. ( - ∞ ; - 2 ) ∪ ( 6 ; + ∞ )
B. ( - ∞ ; - 6 ) ∪ ( - 2 ; + ∞ )
C. ( 2 ; 6 )
D. ( - 6 ; - 2 )
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ

Tập hợp tất cả các giá trị thực của tham số m để phương trình f(cos2x)-2m-1=0 có nghiệm thuộc khoảng - π 3 ; π 4 là
A. 0 ; 1 2
B. 0 ; - 1 2
C. 1 4 ; 1 2
D. - 10 ; 1 2
Cho hàm số y = f(x) liên tục trên các khoảng − ∞ ; 0 v à 0 ; + ∞ , có bảng biến thiên như sau
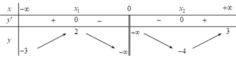
Tìm m để phương trình f x = m có 4 nghiệm phân biệt.
A. -3 < m < 2
B. -3 < m < 3
C. -4 < m < 2
D. -4 < m < 3
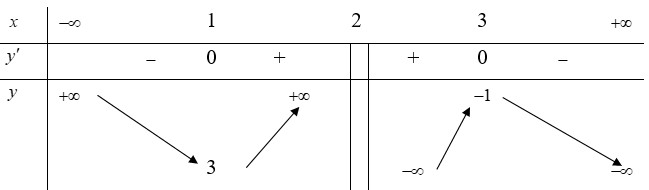
Cho hàm số y=f(x) xác định, liên tục trên R\{1} và có bảng biến thiên như sau
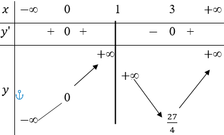
Điều kiện của m để phương trình f(x)=m có 3 nghiệm phân biệt
A. m < 0
B. m > 0
C. m < 0 < 27 4
D. m > 27 4
Cho hàm số y=f(x) liên tục trên ℝ và có bảng biên thiên như sau:
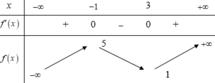
Phương trình f(x) - 2=0 có tất cả bao nhiêu nghiệm?
A. 1
B. 3
C. 2
D. 0