Đáp án A
Điểm M ∈ C ⇒ M a ; a − 3 a + 3
suy ra d M ; O x = a − 3 a + 3 và d M ; O y = a
Do đó T = a + a − 3 a + 3 = a 2 + 2 a − 3 a + 1 ≥ 2.
Dấu “=” xảy ra ⇔ a = 1 ⇒ b = − 1
Vậy T = − 2
Đáp án A
Điểm M ∈ C ⇒ M a ; a − 3 a + 3
suy ra d M ; O x = a − 3 a + 3 và d M ; O y = a
Do đó T = a + a − 3 a + 3 = a 2 + 2 a − 3 a + 1 ≥ 2.
Dấu “=” xảy ra ⇔ a = 1 ⇒ b = − 1
Vậy T = − 2
Cho hàm số y = x − 3 x + 1 (C) và điểm M a ; b thuộc đồ thị (C). Đặt T = 3 ( a + b ) + 2 a b , khi đó để tổng khoảng cách từ điểm M đến hai trục toạ độ là nhỏ nhất thì mệnh đề nào sau đây là đúng?
A. − 3 < T < − 1.
B. − 1 < T < 1.
C. 1 < T < 3.
Cho hàm số y = x − 1 x + 1 có đồ thị (C), điểm M di động trên (C). Gọi d là tổng khoảng cách từ M đến hai trục tọa độ. Khi đó giá trị nhỏ nhất của d là
A. 207 250 .
B. 2 − 1.
C. 2 2 − 1.
D. 2 2 − 2.
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi M x M ; y M là điểm bất kỳ trên (D). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất thì tổng x M + y M bằng:
A. 2 2 - 1
B. 1
C. 2 - 2
D. 2 - 2 2
Cho hàm số y=f(x) có đồ thị y=f'(x) cắt trục Ox hoành tại ba điểm có hoành độ -2<a<b như hình vẽ. Biết rằng f(-2)+f(1)=f(a)+f(b). Để hàm số y = f ( x + m ) có 7 điểm cực trị thì mệnh đề nào dưới đây là đúng
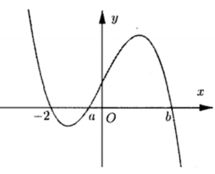
A. f(a)>0>f(-2)
B. f(-2)>0>f(a)
C. f(b)>0>f(a)
D. f(b)>0>f(-2)
Đường thẳng d: y=x+4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4 tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3). Mệnh đề nào sau đây là đúng?
A. m ∈ - ∞ ; 0
B. m ∈ 0 ; 2
C. m ∈ 2 ; 4
D. m ∈ 4 ; + ∞
Cho hàm số y = f(x) có đồ thị y = f’(x) cắt trục Ox tại 3 điểm có hoành độ a<b<c như hình vẽ. Mệnh đề nào dưới đây là đúng
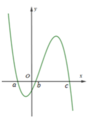
A. f(a)>f(b)>f(c)
B. f(c)>f(b)>f(a)
C. f(c)>f(a)>f(b)
D. f(b)>f(a)>f(c)
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;-2;-3); B(1;1;1) và hai đường thẳng ∆ 1 : x - 2 1 = y - 2 4 = z + 6 - 3 ; ∆ 2 : x - 2 1 = y + 3 - 4 = z - 4 3 . Gọi m là số mặt phẳng (P) tiếp xúc với mặt cầu đường kính AB đồng thời song song với cả hai đường thẳng ∆1;∆2; n là số mặt phẳng (Q), sao cho khoảng cách từ A đến (Q) bằng 15, khoảng cách từ B đến (Q) bằng 10. Chọn mệnh đề đúng trong các mệnh đề sau.
A. m + n = 1
B. m + n = 4
C. m + n = 3
D. m + n = 2
Cho hàm số y = x + 1 x - 1 có đồ thị là (C). Gọi M x M ; y M là một điểm bất kỳ trên (C). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất, tính tổng x M + y M
A. 2 - 2
B. 2 2 - 1
C. 1.
D. 2 - 2 2