Đáp án C.
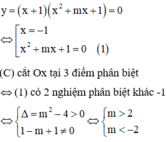
Số nguyên dương m nhỏ nhất thỏa mãn là 3.
Đáp án C.
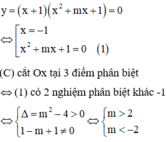
Số nguyên dương m nhỏ nhất thỏa mãn là 3.
Để đồ thị hàm số ( C ) : y = x 3 - 2 x 2 + ( 1 - m ) x + m (m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 < 4 thì giá trị của m là:
A. m < 1
B. m > 1 m < - 1 4
C. - 1 4 < m < 1
D. - 1 4 < m < 1 m ≠ 0
Cho hàm số y = x − 2 x − 3 có đồ thị (C). Tìm m để đường thẳng d đi qua A ( 0 ; m ) có hệ góc bằng 2 cắt (C) tại 2 điểm phân biệt có hoành độ dương
A. m ∈ ℝ .
B. 2 3 < m < 7 .
C. m < 2 3 .
D. m > 7 .
Cho hàm số: y = x − 1 x 2 + m x + m . Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt:
A. m > 4 m < 0
B. − 1 2 ≠ m < 0
C. 0 < m < 4
D. − 1 2 ≠ m < 0 m > 4
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 - m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt
A. 3
B. 2
C. 4
D. 1
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C) và đường thẳng d : y = x + m . Tìm tất cả các tham số m dương để đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt A,B sao cho A B = 10 .
A. m = 2 .
B. m =1.
C. m = 0.
D. m = 0 và m = 2 .
Cho hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 có đồ thị là (Cm) với m là tham số. Có bao nhiêu giá trị của m nguyên trong đoạn [–10;100] để (Cm) cắt trục hoành tại ba điểm phân biệt A(2;0), B, C sao cho trong hai điểm B, C có một điểm nằm trong và một điểm nằm ngoài đường tròn có phương trình x2 + y2 = 1?
A. 109
B. 108
C. 18
D. 19
Cho hàm số y = x 3 + 2 ( m + 1 ) x 2 + 3 mx + 2 có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d:y=-x +2 cắt đồ thị (C ) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2 6 .
A.m= -2.
B. m= -2 hoặc m= 3.
C. m= 3.
D. Không tồn tại m.
Cho hàm số f ( x ) = x 3 - ( m 2 + m + 1 ) x + m 2 + m có đồ thị cắt trục hoành tại ba điểm có hoành độ x 1 , x 2 , x 3 . Biết m là số nguyên dương, giá trị nhỏ nhất của biểu thức P = x 1 2 + x 2 2 + x 3 2 gần giá trị nào sau đây nhất
A. 2
B. 13/2
C. 6
D. 12
Cho hàm số y = x 4 - m - 1 x 2 + m - 2 . Tìm m để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt.
A. mÎ(1; +¥)
B. mÎ(2; +¥ )
C. mÎ(2; +¥) \{3}
D. mÎ(2;3)