Các câu hỏi tương tự
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
l
n
(
2
x
2
+
e
2
)
trên [0;e]. Mệnh đề nào sau đây đúng A. M + m 5 B. M + m 4 + ln3 C. M + m 4 + ln2 D. M + m 2 + ln3
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = l n ( 2 x 2 + e 2 ) trên [0;e]. Mệnh đề nào sau đây đúng
A. M + m = 5
B. M + m = 4 + ln3
C. M + m = 4 + ln2
D. M + m = 2 + ln3
Cho hàm số
y
ln
x
-
4
ln
x
-
2
m
với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đổng biến trên khoảng (1;e). Tìm số phần tử của S. A. 2. B. 4. C. 3. D. 1.
Đọc tiếp
Cho hàm số y = ln x - 4 ln x - 2 m với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đổng biến trên khoảng (1;e). Tìm số phần tử của S.
A. 2.
B. 4.
C. 3.
D. 1.
Cho hàm số
y
f
(
x
;
m
)
có đồ thị hàm số
y
f
(
x
;
m
)
như hình vẽ Biết
f
(
a
)
f
(
c
)
0
;
f
(
b
)
0
f
(
e
)
Hỏi hàm số...
Đọc tiếp
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
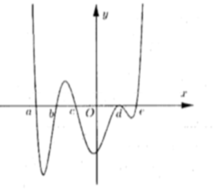
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho các phát biểu sau(1) Đơn giản biểu thức
M
a
1
4
-
b
1
4
a
1
4
+
b
1...
Đọc tiếp
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Đồ thị hàm số
y
-
x
3
+
3
m
x
+
1
có 2 điểm cực trị A,B
x
A
x
B
sao cho tứ giác ABOE là hình bình hạnh với O là gốc tọa độ và điểm E(-4;-32). Tìm tất cả các giá trị thực của tham số m. A. m 1 B. m 4 C. m 2 D.
m...
Đọc tiếp
Đồ thị hàm số y = - x 3 + 3 m x + 1 có 2 điểm cực trị A,B x A < x B sao cho tứ giác ABOE là hình bình hạnh với O là gốc tọa độ và điểm E(-4;-32). Tìm tất cả các giá trị thực của tham số m.
A. m = 1
B. m = 4
C. m = 2
D. m ∈ ∅
Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
.
e
−
x
trên đoạn
−
1
;
1
. Tính tổng M+N. A.
M
+
N
3
e
B.
M
+...
Đọc tiếp
Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 . e − x trên đoạn − 1 ; 1 . Tính tổng M+N.
A. M + N = 3 e
B. M + N = e
C. M + N = 2 e − 1
D. M + N = 2 e + 1
Cho hàm số \(y=x^3+3x^2+mx+1\)\(\left(C_m\right)\)
Tìm m để \(\left(C_m\right)\) cắt đường thẳng y=1 tại 3 điểm phân biệt C (0;1), D, E. Tìm m để các tiếp tuyến tại D, E vuông góc với nhau
Cho hàm số
y
x
4
-
2
(
m
+
1
)
x
2
+
m
+
2
có đồ thị (C) . Gọi
∆
là tiếp tuyến với đồ thị (C) tại điểm thuộc (C) có hoành độ bằng 1. Với giá trị nào của tham số m thì
∆
vuông góc với đường thẳng d:
y
-
1
4
x
-
2016
A. m-1 B. m0 C. m1 D. m2
Đọc tiếp
Cho hàm số y = x 4 - 2 ( m + 1 ) x 2 + m + 2 có đồ thị (C) . Gọi ∆ là tiếp tuyến với đồ thị (C) tại điểm thuộc (C) có hoành độ bằng 1. Với giá trị nào của tham số m thì ∆ vuông góc với đường thẳng d: y = - 1 4 x - 2016
A. m=-1
B. m=0
C. m=1
D. m=2
Giả sử đường thẳng yx+m cắt đồ thị (C) của hàm số
y
x
−
1
1
−
2
x
tại hai điểm phân biệt E và F. Gọi
k
1
,
k
2
lần lượt là hệ số góc của các tiếp tuyến với (C) tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức
S...
Đọc tiếp
Giả sử đường thẳng y=x+m cắt đồ thị (C) của hàm số y = x − 1 1 − 2 x tại hai điểm phân biệt E và F. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức S = k 1 4 + k 2 4 − 3 k 1 k 2 .
A. min S = − 1
B. min S = − 5 8
C. min S = 135
D. min S = − 25 81
Giả sử đường thẳng
y
x
+
m
cắt đồ thị (C) của hàm số
y
x
−
1
1
−
2
x
tại hai điểm phân biệt E và F. Gọi
k
1
,
k
2
lần lượt là hệ số góc của các tiếp tuyến với
C
tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức
S...
Đọc tiếp
Giả sử đường thẳng y = x + m cắt đồ thị (C) của hàm số y = x − 1 1 − 2 x tại hai điểm phân biệt E và F. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với C tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức S = k 1 4 + k 2 4 − 3 k 1 k 2 .
A. min S = − 1
B. min S = − 5 8
C. min S = 135
D. min S = − 25 81





