Đáp án A
Ta có: Đồ thị đi qua điểm (0,c) suy ra c = − 3
Tại x = 1 ⇒ y = a + b + c = − 5 ⇒ a + b = − 2
Do x = 1 là điểm cực trị suy ra y ' 1 = 0 ⇔ 4 a + 2 b = 0
Do đó c = − 3 a = 2 b = − 4 ⇒ P = − 15
Đáp án A
Ta có: Đồ thị đi qua điểm (0,c) suy ra c = − 3
Tại x = 1 ⇒ y = a + b + c = − 5 ⇒ a + b = − 2
Do x = 1 là điểm cực trị suy ra y ' 1 = 0 ⇔ 4 a + 2 b = 0
Do đó c = − 3 a = 2 b = − 4 ⇒ P = − 15
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c , d ∈ ℝ ) có bảng biến thiên như hình sau:
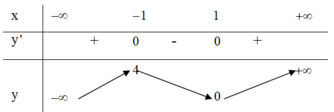
Tìm tất cả giá trị thực của tham số m để phương trình m = f ( x ) có 4 nghiệm phân biệt trong đó có đúng một nghiệm dương.
A.m > 2
B.0 < m < 4
C.m > 0
D.2 < m < 4
Cho hàm số y=f(x). Hàm số y=f '(x) có bảng biến thiên như hình vẽ dưới
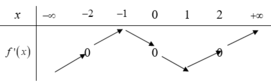
Giá trị lớn nhất của hàm số g ( x ) = f ( 2 x ) - sin 2 x trên [-1;1]
A. f(-1)
B. f(0)
C. f(2)
D. f(1)
Cho hai hàm số f(x) và g(x) có đồ thị như hình vẽ dưới đây
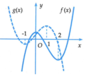
Biết rằng hai hàm số y = f - 2 x + 1 và y = 3 g a x + b a , b ∈ Q có cùng khoảng đồng biến. Giá trị của biểu thức a + 2 b bằng
A. a + 2 b = 3
B. a + 2 b = 4
C. a + 2 b = 2
D. a + 2 b = 6
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây
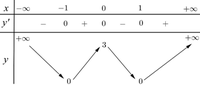
Hàm số có giá trị cực tiểu bằng
A. -1
B. 0
C. 3
D. 1
Cho hàm số y = f x . Hàm số y = f ' x có bảng biến thiên như hình vẽ dưới
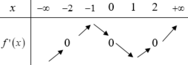
Giá trị lớn nhất của hàm số g x = f 2 x - sin 2 x trên [ -1;1]
A. f - 1
B. f 0
C. f 2
D. f 1
Cho hàm số y = x − a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức P=a+b+c
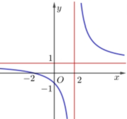
A. P = - 3
B. P = 1
C. P = 5
D. P = 2
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng biến thiên như hình vẽ dưới đây
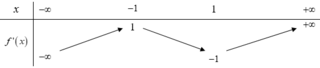
Hàm số g(x)=f(x)-x có bao nhiêu điểm cực trị?
A. 3
B. 2
C. 0
D. 1
Cho hàm số y=f (x) có bảng biến thiên như hình bên dưới. Giá trị cực tiểu của hàm số là
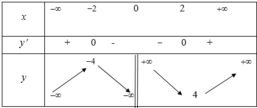
A. 4
B. - 4
C. - 2
D. 2