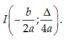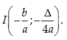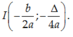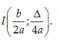Các câu hỏi tương tự
Gọi (P) là đồ thị hàm số
y
a
x
2
+
c
. Để đỉnh của (P) có tọa độ (0; -3) và một trong hai giao điểm của (P) với trục hoành là điểm có hoành độ bằng -5 thì: A.
a
3
25
,
c
3
B.
a
-...
Đọc tiếp
Gọi (P) là đồ thị hàm số y = a x 2 + c . Để đỉnh của (P) có tọa độ (0; -3) và một trong hai giao điểm của (P) với trục hoành là điểm có hoành độ bằng -5 thì:
A. a = 3 25 , c = 3
B. a = - 3 25 , c = - 3
C. a = - 3 25 , c = 3
D. a = 3 25 , c = - 3
cho đồ thị hàm số y=ax2+bx+4 có đỉnh là điểm I(1,-2). Tính a+3b
A.20
B.-18
C.-3-
D.25
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Cho P: y=ax2+bx+1. Tìm a,b để:
(P) đi qua B(-1;6) và có tung độ đỉnh là -3.
a. Xét dấu của biểu thức f(x) 2x(x+2)-(x+2)(x+1)b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y 2x(x+2) ( C1 ) và y (x+2)(x+1)(C2)Tính tọa độ giao điểm A và B của (C1) và (C2).c. Tính các hệ số a, b, c để hàm số y ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
Đọc tiếp
a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)
b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)
Tính tọa độ giao điểm A và B của (C1) và (C2).
c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
tìm hàm số bậc hai y=ax2 + bx + c có đồ thị của nó có đỉnh I(-2;1) và cắt đưởng thẳng y=x-1 tại 1 điểm trên trục tung
Cho hàm số y=\(ax^2+bx+c\) (a≠0) có đồ thị (P).Biết đồ thị của hàm số có đỉnh I(1;1) và đi qua điểm A(2;3). Tính tổng S=a2+b2+c2
A.3 B.4 C.29 D.1
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
Cho hàm số y ax2 + bx + c có đồ thị (P) như hình vẽ.Khẳng định nào sau đây là sai? A. Hàm số đồng biến trên khoảng (−
∞
; 3). B. (P) có đỉnh là I (3; 4). C. (P) cắt trục tung tại điểm có tung độ bằng 1. D. (P) cắt trục hoành tại hai điểm phân biệt.
Đọc tiếp
Cho hàm số y = ax2 + bx + c có đồ thị (P) như hình vẽ.

Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng (− ∞ ; 3).
B. (P) có đỉnh là I (3; 4).
C. (P) cắt trục tung tại điểm có tung độ bằng 1.
D. (P) cắt trục hoành tại hai điểm phân biệt.
Nếu hàm số y ax2+ bx+c có đồ thị như sau thì dấu các hệ số của nó là: A.a0; b0; c 0 B.a 0; b0; c 0 C. a0; b0; c 0 D. A0; b0; c 0
Đọc tiếp
Nếu hàm số y= ax2+ bx+c có đồ thị như sau thì dấu các hệ số của nó là:
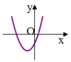
A.a>0; b>0; c> 0
B.a> 0; b>0; c< 0
C. a>0; b<0; c> 0
D. A>0; b<0; c< 0