Các câu hỏi tương tự
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ). Diện tích hình phẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x 0; x 2 có diện tích bằng
28
5
(phần gạch chéo tro...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm
A
−
1
;
0
. Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0, x2 bằng...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
x
+
1
x
-
1
có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng A. 16. B. 32. C. 8. D. 4.
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng
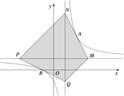
A. 16.
B. 32.
C. 8.
D. 4.
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0, x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ) A.
2...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0, x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ)
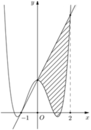
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1 D. -3
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1
D. -3
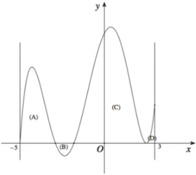
Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A), (B), (C), (D) giới hạn bởi đồ thị hàm số f(x) và trục hoành lần lượt bẳng 6; 3; 12; 2. Tích phân
∫
-
3
1
2
f
2
x
+
1
+...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A), (B), (C), (D) giới hạn bởi đồ thị hàm số f(x) và trục hoành lần lượt bẳng 6; 3; 12; 2. Tích phân ∫ - 3 1 2 f 2 x + 1 + 1 d x bằng
A. 27
B. 25
C. 17
D. 21
Biết điểm A có hoành độ lớn hơn – 4 là giao điểm của đường thẳng
y
x
+
7
với đồ thị (C) của hàm số
y
2
x
-
1
x
+
1
. Tiếp tuyến của đồ thì (C) tại điểm A cắt hai trục độ Ox, Oy lần lượt tịa E, F. Khi đó tam giác OEF (O là gốc tạo độ) có diện tích bằng: A. ...
Đọc tiếp
Biết điểm A có hoành độ lớn hơn – 4 là giao điểm của đường thẳng y = x + 7 với đồ thị (C) của hàm số y = 2 x - 1 x + 1 . Tiếp tuyến của đồ thì (C) tại điểm A cắt hai trục độ Ox, Oy lần lượt tịa E, F. Khi đó tam giác OEF (O là gốc tạo độ) có diện tích bằng:
A. 33 2
B. 121 2
C. 121 3
D. 121 6
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số
y
log
a
x
,
y
log
a
x
,
y
log
a
3
x...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x , y = log a 3 x , với x > 0 , a > 1 . Giá trị của a là:
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6