Đáp án D
Dựa vào đồ thị hàm số dễ dàng nhận biết a > 0,c > 0. Đồ thị hàm số có 3 điểm cực trị nên a,b trái dấu. Từ đó ta có a > 0 , b < 0 , c > 0 .
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = x ,y=0 và x=4 quanh trục Ox. Đường thẳng x=a (0<a<4) cắt đồ thị hàm số y = x tại M (hình vẽ bên). Gọi V 1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V=2 V 1 . Khi đó
A. a = 2 2
B. a = 5 2
C. a = 2
D. a = 3
Cho các số thực a,b sao cho 0 < a , b ≠ 1 , biết rằng đồ thị các hàm số y = a x và y = log b x cắt nhau tại điểm M ( 2018 ; 2019 − 1 5 ) . Mệnh đề nào dưới đây đúng?
A. a > 1 , b > 1.
B. a > 1 , 0 < b < 1.
C. 0 < a < 1 , b > 1.
D. 0 < a < 1 , 0 < b < 1.
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(-1)>0<f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x),y=0,x=-1 và x=1. Mệnh đề nào sau đây đúng?
A. S = ∫ - 1 0 f ( x ) d x + ∫ 0 1 | f ( x ) | d x
B. S = ∫ - 1 1 | f ( x ) | d x
C. S = ∫ - 1 1 f ( x ) d x
D. S = ∫ - 1 1 f ( x ) d x
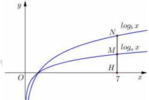
Cho hàm số y = l o g a x v à y = l o g b x có đồ thị như hình vẽ bên. Đường thẳng x=7 cắt trục hoành, đồ thị hàm số y = l o g a x và y = l o g b x lần lượt tại H, M và N. Biết rằng HM=MN. Mệnh đề nào sau đây là đúng?
A. a = 7b
B. a = b 2
C. a = b 7
D. a = 2b
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ ℝ ) thỏa mãn a > 0 , d > 0 > 2018 , a + b + c + d - 2018 < 0 Tìm số điểm cực trị của hàm số y = f ( x ) - 2018
A. 2
B. 1
C. 3
D. 5
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c = 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P).
A. 2017
B. 2014 3
C. 2016 3
D. 2015 3
1. Chứng minh rằng mọi số a, b, c khác 0 tồn tại 1 trong các phương trình sau phải có ngiệm:
ax2 + 2bc + c = 0 (1)
bx2 + 2cx + a = 0 (2)
cx2 + 2ax + b = 0 (2)
Lớp 9
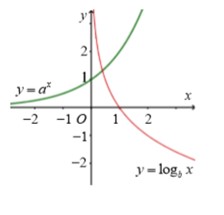
Cho a > 0 , b > 0 , b ≠ 0 . Đồ thị các hàm số y = a x và y = log b x cho như hình vẽ bên. Mệnh đề nào sau đây là đúng
A. a>1, 0<b<1
B. 1>a>0; b>1
C. 0<a<1; 0<b<1
D. a>1; b>1
