Các câu hỏi tương tự
Cho a, b, x, y là các số thực dương thỏa mãn
a
≠
1
,
b
≠
1
,
x
2
+
y
2
1.
Biết rằng
log
a
x
+
y
0
và
log
b
x...
Đọc tiếp
Cho a, b, x, y là các số thực dương thỏa mãn a ≠ 1 , b ≠ 1 , x 2 + y 2 = 1. Biết rằng log a x + y > 0 và log b x y < 0 . Mệnh đề nào sau đây đúng?
A. 0 < a < 1 v à b > 1
B. a > 1 v à b > 1
C. 0 < a < 1 v à 0 < b < 1
D. a > 1 v à 0 < b < 1
Cho
a
,
b
0
;
a
,
b
≠
1
và x, y là hai số thực dương. Trong các mệnh đề dưới đây, mệnh đề nào sai? A.
log
a
x
y
log
a
x
+
log
a
y
.
B. ...
Đọc tiếp
Cho a , b > 0 ; a , b ≠ 1 và x, y là hai số thực dương. Trong các mệnh đề dưới đây, mệnh đề nào sai?
A. log a x y = log a x + log a y .
B. log b a . log a x = log b x .
C. log a 1 x = 1 log a x .
D. log a x y = log a x − log a y .
Cho các mệnh đề sau:(I). Nếu
a
b
c
t
h
ì
2
ln
a
ln
b
+
ln
c
(II). Cho số thực 0 a ≠ 1. Khi đó
a
-
1
log
a
x
≥
0...
Đọc tiếp
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Cho hàm số
y
x
3
−
3
m
x
+
1
1
.
Cho A(2;3) tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A A. m1/2 B. m-3/2 C. m-1/2 D. m3/2
Đọc tiếp
Cho hàm số y = x 3 − 3 m x + 1 1 . Cho A(2;3) tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A
A. m=1/2
B. m=-3/2
C. m=-1/2
D. m=3/2
Cho 3 số
a
,
b
,
c
0
,
a
≠
1
,
b
≠
1
,
c
≠
1.
Đồ thị các hàm số
y
a
x
,
y
a
x
,
y
c
x
được cho trong hình vẽ dưới.Mệnh đề nà...
Đọc tiếp
Cho 3 số a , b , c > 0 , a ≠ 1 , b ≠ 1 , c ≠ 1. Đồ thị các hàm số y = a x , y = a x , y = c x được cho trong hình vẽ dưới.

Mệnh đề nào sau đây đúng?
A. b < c < a
B. a < c < b
C. a < b < c
D. c < a < b
Cho 3 số a, b, c 0,
a
≠
1
,
b
≠
1
,
c
≠
1
. Đồ thị các hàm số
y
a
x
,
y
b
x
,
c
c
x
. được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng ? A. b c a B. a c b C. a b c D. c a b
Đọc tiếp
Cho 3 số a, b, c > 0, a ≠ 1 , b ≠ 1 , c ≠ 1 . Đồ thị các hàm số y = a x , y = b x , c = c x . được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng ?
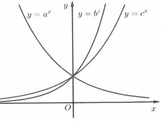
A. b < c < a
B. a < c < b
C. a < b < c
D. c < a < b
Cho
0
a
≠
1
và
0
b
≠
1
. Đồ thị hàm số
y
a
x
và
y
log
b
x...
Đọc tiếp
Cho 0 < a ≠ 1 và 0 < b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?

A. a >1, b >1
B. a >1, 0 <b <1
C. 0 <a <1, b >1
D. 0 <a <1, 0 <b <1
Cho
a
0,
b
0,
a
≠
1,
b
≠
1
. Đồ thị hàm số
y
a
x
và
y
log
b
x
được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng? A.
a
1
;
0
b
1....
Đọc tiếp
Cho a > 0, b > 0, a ≠ 1, b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng?
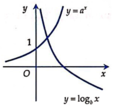
A. a > 1 ; 0 < b < 1.
B. 0 < a < 1 ; b > 1.
C. 0 < a < 1 ; 0 < b < 1.
D. a > 1 ; b > 1.
Với các số thực
a
,
b
,
c
0
và
a
,
b
≠
1
bất kì. Mệnh đề nào dưới đây sai A.
log
a
b
....
Đọc tiếp
Với các số thực a , b , c > 0 và a , b ≠ 1 bất kì. Mệnh đề nào dưới đây sai
A. log a b . c = log a b + log a c
B. log a b = c log a b a
C. log a b . log b c = log a c
D. log a b = 1 log b a




