Chọn C.
Ta có: y ' = x 2 + 2 mc + 2 m - 1 . Để hàm số có cực trị thì phương trình y'= 0 có hai nghiệm phân biệt
⇔ Δ ' > 0 ⇔ m 2 - 2 m + 1 > 0 ⇔ ( m - 1 ) 2 > 0 ⇔ m ≠ 1 .
Chọn C.
Ta có: y ' = x 2 + 2 mc + 2 m - 1 . Để hàm số có cực trị thì phương trình y'= 0 có hai nghiệm phân biệt
⇔ Δ ' > 0 ⇔ m 2 - 2 m + 1 > 0 ⇔ ( m - 1 ) 2 > 0 ⇔ m ≠ 1 .
Cho hàm số y = f x = x 3 − 3 x 2 + m x + 1. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số f x có 3 điểm cực trị.
A. m=-1
B. m=2
C. m=0
D. m=1
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số y = f ( x ) = x 3 - ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tất cả các giá trị của tham số m để hàm số y=f(|x|) có 5 điểm cực trị
A. 5 4 < m ≤ 2
B. - 2 < m < 5 4
C. - 5 4 < m < 2
D. 5 4 < m < 2
Cho hàm số y = m + 2 x 3 + 3 x 2 + m x − 5 . Tìm tất cả các giá trị của tham số thực m để điểm cực đại, cực tiểu của hàm số đã cho có hoành độ là một số dương.
A. -3 < m < -2
B. -3 < m < 1
C. m < -2
D. m < 0
Tìm tất cả các giá trị tham số m để hàm số y = x 2 + ( 2 - m ) x - m + 2 x + 1 có 4 cực trị.
A. - 2 ≤ m ≤ 3 .
B. - 2 < m ≤ 3 .
C. m> 2 hoặc m< -2
D. m> 2 hoặc m< -3
Tìm tất cả các giá trị của tham số m để hàm số
f x = m - 1 3 x 3 - m + 3 2 x 2 + 3 - m x - m + 3 2
có cực trị và số 2 nằm giữa hai điểm cực trị của hàm số
A. 1 < m ≤ 7
B. 1 ≤ m < 7
C. 1 < m < 7
D. 1 ≤ m ≤ 7
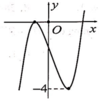
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x - 1 ) - m - 1 có 3 điểm cực trị?
A. -1<m<5
B. - 1 ≤ m ≤ 5
C. m ≥ - 1 hoặc m ≤ - 5
D. m>-1 hoặc m<-5
Tìm tất cả các giá trị của tham số thực m để hàm số y = − x 3 − 2 x 2 + m x + 1 đạt cực tiểu tại điểm x = -1
A. m < -1
B. m ≠ − 1
C. m = -1
D. m > -1
Cho hàm số y = f x = x 3 - 2 m - 1 x 2 + 2 - m x + 2 . Tìm tất cả các giá trị của tham số m để hàm số y = f x có 5 điểm cực trị
A. 5 4 < m ≤ 2
B. - 2 < m < 5 4
C. - 5 4 < m ≤ 2
D. 5 4 < m < 2