- Ta có :
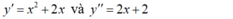
- Theo giả thiết x 0 là nghiệm của phương trình:
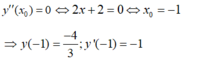
- Phương trình tiếp tuyến tại điểm 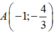 là:
là:
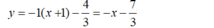
Chọn A.
- Ta có :
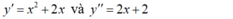
- Theo giả thiết x 0 là nghiệm của phương trình:
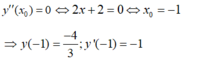
- Phương trình tiếp tuyến tại điểm 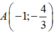 là:
là:
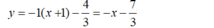
Chọn A.
Cho hàm số y = 1 3 x 3 + x 2 - 2 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y" = 0 là:
A. y = - x - 7 3
B. y = - x + 7 3
C. y = x - 7 3
D. y = 7 3 x
Cho hàm số 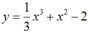 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y” = 0 là
có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y” = 0 là
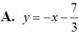
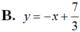
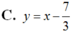
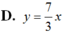
Qua điểm A(0;2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x 4 – 2 x 2 + 2 .
A. 2
B. 3
C. 0
D. 1
Cho hàm số y = x 2 + m ( 2018 - x 2 + 1 ) - 2021 với m là tham số thực. Gọi S là tổng tất cả các giá trị nguyên của tham số m để đồ thị của hàm số đã cho cắt trục hoành tại đúng hai điểm phân biệt. Tính S.
A. 960
B. 986
C. 984
D. 990
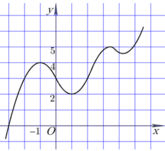
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình
f
(
x
2
-
2
x
)
=
m
có đúng 4 nghiệm thực phân biệt thuộc đoạn
[
-
3
2
;
7
2
]
.
A. 1
B. 4
C. 2
D. 3
Cho bốn hàm số: y = sin x , y = x 1 3 , y = x 2 + x + 1 , y = 2 x + 1 x 2 + 1 .
Số các hàm số có tập xác định là R bằng:
A.3
B.2
C.1
D.4
Tính đạo hàm của hàm số sau: y = (x2 – x + 1)3.(x2 + x + 1)2
A: (x2 – x + 1)2(x2 + x + 1)
B: (x2 – x + 1)2(x2 + x + 1)[(2x + 3)(x + x2)]
C: (x2 – x + 1)2(x2 + x + 1)[3(2x - 1) + 2(2x + 1)]
D: Tất cả sai
Đạo hàm của hàm số sau là đa thức bậc mấy: y = (1 + 2x)(2 + 3x2)(3 – 4x3).
A: 3
B: 4
C: 5
D: 6
Tính đạo hàm các hàm số sau:
a) $y={{x}^{3}}-3{{x}^{2}}+2020x$.
b) $y=\cos 3x-\sin x$.