Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm 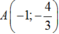 là: y = -1.(x + 1) - 7/3
là: y = -1.(x + 1) - 7/3
Hay  .
.
Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm 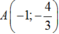 là: y = -1.(x + 1) - 7/3
là: y = -1.(x + 1) - 7/3
Hay  .
.
Cho hàm số y = 1 3 x 3 + x 2 - 2 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y" = 0 là:
A. y = - x - 7 3
B. y = - x + 7 3
C. y = x - 7 3
D. y = 7 3 x
Cho hàm số y = 1 3 x 3 + x 2 - 2 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y" = 0 là:
A. y = - x - 7 3
B. y = - x + 7 3
C. y = x - 7 3
D. y = 7 3 x
Cho hàm số y = x 2 + m ( 2018 - x 2 + 1 ) - 2021 với m là tham số thực. Gọi S là tổng tất cả các giá trị nguyên của tham số m để đồ thị của hàm số đã cho cắt trục hoành tại đúng hai điểm phân biệt. Tính S.
A. 960
B. 986
C. 984
D. 990
Qua điểm A(0;2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x 4 – 2 x 2 + 2 .
A. 2
B. 3
C. 0
D. 1
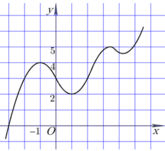
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình
f
(
x
2
-
2
x
)
=
m
có đúng 4 nghiệm thực phân biệt thuộc đoạn
[
-
3
2
;
7
2
]
.
A. 1
B. 4
C. 2
D. 3
Cho bốn hàm số: y = sin x , y = x 1 3 , y = x 2 + x + 1 , y = 2 x + 1 x 2 + 1 .
Số các hàm số có tập xác định là R bằng:
A.3
B.2
C.1
D.4
Tập xác định của hàm số y = tan 2 x là:
![]()

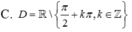
![]()
Đạo hàm của hàm số sau là đa thức bậc mấy: y = (1 + 2x)(2 + 3x2)(3 – 4x3).
A: 3
B: 4
C: 5
D: 6
a. cho cấp số cộng Un biết U5=18 và 4Sn=S2n tìm số hạn đầu u1 và công sai d của cấp số cộng
b. cho ba số a,b,c là ba số liên tiếp của một cấp số cộng có công sai là 2. Nếu tăng số thứ nhất thêm 1, tăng số thứ 2 thêm 1 và số thứ ba thêm 3 thì được ba số mới là ba số liên tiếp của một cấp số nhân. Tính a+b+c