Đáp án D
- Phương pháp: Sử dụng công thức tính đạo hàm của tích 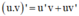
- Cách giải:
+ Ta có:
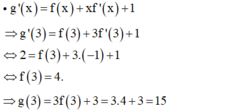
Đáp án D
- Phương pháp: Sử dụng công thức tính đạo hàm của tích 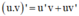
- Cách giải:
+ Ta có:
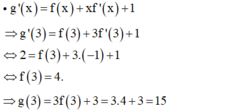
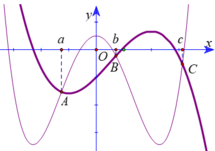
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
Cho hàm số: f x = 2 v ớ i x ≤ 3 a x - b v ớ i 3 < x < 5 6 v ớ i x ≥ 5
Với giá trị nào của a,b thì hàm số f(x) liên tục trên R?
A. a = 2 và b = 8
B. a = 4 và b = -10
C. a = 2 và b = 4
D. a = 2 và b = -4
cho hàm số y = f(x) = acos(x) -b và y = g(x) = asin(x) +2b -3 và a là số dương. tính a+b sao cho GTLN f(x) =1, GTNN g(x) =3
A. 8
B. 23
C. 15
D.7
GIẢI TỰ LUẬN HỘ MK NHA
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Cho hàm số f(x) có đạo hàm trên ℝ và có đồ thị y=f'(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (-1;0).
B. Hàm số g(x) nghịch biến trên. ( - ∞ ; - 2 )
C. Hàm số g(x) nghịch biến trên. ( 0 ; 2 )
D. Hàm số g(x) đồng biến trên. ( 2 ; + ∞ )
Cho hàm số f ( x ) = x 2 2 k h i x ≤ 1 ã + b k h i x > 1 . Với giá trị nào sau đây của a,b thì hàm số có đạo hàm tại x = 1?
A. a = 1 ; b = - 1 2
B. a = 1 2 ; b = 1 2
C. a = 1 2 ; b = - 1 2
D. a = 1 ; b = 1 2