Các câu hỏi tương tự
Cho hàm số f(x) a
x
2
+ bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình |f(x)| − 1 m có đúng 2 nghiệm phân biệt. A.
m
≥
0
m
−
1
B. ...
Đọc tiếp
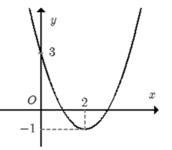
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình |f(x)| − 1 = m có đúng 2 nghiệm phân biệt.
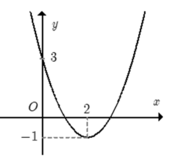
A. m ≥ 0 m = − 1
B. m > 0 m = − 1
C. m ≥ -1
D. m ≥ 0
Cho hàm số f(x) a
x
2
+ bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| m có đúng 4 nghiệm phân biệt. A. 0 m 1. B. m 3. C. m −1, m 3. D. −1 m
m
0
.
Đọc tiếp
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.
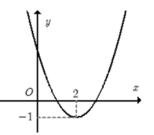
A. 0 < m < 1.
B. m > 3.
C. m = −1, m = 3.
D. −1 < m < m 0 .
3: cho hàm số f(x)=ax^2+bx+c có tọa độ đỉnh (2;-1) và có giá trị nhỏ nhất khi là -1 khi x=2
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x-2018)-2|=m có đúng 3 nghiệm.
Cho hàm số y = f(x) có bảng biến thiên như sau:
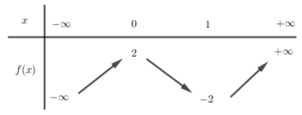
Với giá trị nào của tham số m thì phương trình |f(x) − 1| = m có bốn nghiệm phân biệt.
A. m = 1.
B. 1 < m < 3.
C. 0 < m < 1.
D. m ≥ 3.
Câu 29: Cho hàm số y= f(x)= ax^2 + bx+c có đồ thị như hình vẽ bên.( dưới bình luận)
Có bao nhiêu giá trị nguyên m để phương trình
f^2(|x|)+(m- 2019) f (|x|)+m– 2020 =0 có 6 nghiệm
phân biệt
Em cần gấp ạ !!!!
a) Số giá trị nguyên của tham số m thuộc (-5;5) để phuong trình x2+2mx+m2+m-3 =0 có 2 nghiệm phân biệt
b)Với giá trị nào của m thì nhị thức bậc nhất f(x)=mx-3 luôn âm với mọi x
Cho hàm số f(x) = \(\left\{{}\begin{matrix}-x+1khix< -2\\2x+7khix\ge-2\end{matrix}\right.\)
a) Lập bảng biến thiên và vẽ đồ thị hàm số trên
b) Tìm m để phương trình f(x)=m có 2 nghiệm phân biệt
c) Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên [-3; 1]
vẽ đồ thị hàm số \(y=f\left(x\right)=\left|x^2-2x-3\right|\). từ đó suy ra tất cả các giá trị của tham số của m để phương trình \(\left|x^2-2x-3\right|=m^4-2m^2+4\) có 4 nghiệm phân biệt
1) Cho hàm số: yx^2-3x+4 có đồ thị là P và đường thẳng d có phương trình:y2x-m, và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt A,B sao cho: OA^2+OB^257 và khi đó O là toa độ góc2) Cho hàm số fleft(xright)sqrt{3-x}-sqrt{3+x}-x^3-x. Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình fleft(2x-1right)fleft(-2aright) có ít nhất là 3 số nguyên
Đọc tiếp
1) Cho hàm số: \(y=x^2-3x+4\) có đồ thị là P và đường thẳng d có phương trình:
\(y=2x-m\), và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt \(A,B\) sao cho: \(OA^2+OB^2=57\) và khi đó O là toa độ góc
2) Cho hàm số \(f\left(x\right)=\sqrt{3-x}-\sqrt{3+x}-x^3-x\). Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình \(f\left(2x-1\right)>f\left(-2a\right)\) có ít nhất là 3 số nguyên