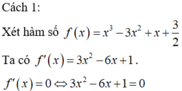Các câu hỏi tương tự
Cho đa thức f(x) = x^2+ax+b; a, b ∈ R. Giả sử phương trình f (f(x)) = 0 có 4 nghiệm thực phân biệt và tổng của hai trong bốn nghiệm đó bằng −1. Chứng minh rằng b ≤ − 1/4
Cho hàm số
f
(
x
)
x
3
+
8
x
+
1
x
-
2
. Phương trình f(x) 0 có nghiệm hay khônga) tr...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + 8 x + 1 x - 2 . Phương trình f(x) = 0 có nghiệm hay không
a) trong khoảng (1; 3)?
b) trong khoảng (-3; 1)?
Cho hàm số f ( x ) = 4 5 x 5 - 6 . Số nghiệm của phương trình f'(x) = 4 là bao nhiêu?
A. 0
B. 1
C. 2
D. Nhiều hơn nghiệm.
Cho hàm số f(x) = 5(x + 1)3 + 4(x + 1). Tập nghiệm của phương trình f ”(x) = 0 là
A. [-1 ; 2] .
B. -1.
C. {-1}.
D. ∅.
Cho hàm số
f
(
x
)
5
(
x
+
1
)
3
+
4
(
x
+
1
)
. Tập nghiệm của phương trình
f
(
x
)
0
là A. [-1;2] B.
(
-
∞
;
0
]
C. {1} D. ...
Đọc tiếp
Cho hàm số f ( x ) = 5 ( x + 1 ) 3 + 4 ( x + 1 ) . Tập nghiệm của phương trình f ' ' ( x ) = 0 là
A. [-1;2]
B. ( - ∞ ; 0 ]
C. {1}
D. ∅
Chứng minh phương trình sau có ít nhất 2 nghiệm phân biệt Với mọi m thuộc R. đặt f(x)=X^4+(m-2)x^3+x^3+(3m+1)x-4m-2016=0
Cho hàm số f ( x ) = x 2 + 5 ; g ( x ) = 9 x - 3 2 x 2 . Số nghiệm của phương trình f'(x) = 4 là bao nhiêu?
A. -4
B. 4
C. 9 5
D. 5 9
Cho f(x)=1/3(m-1)x³-mx²+(m+2)x-5. Tìm m để a)f'(x) lớn hơn hoặc bằng 0 với mọi x b)f'(x) nhỏ hơn hoặc bằng 0 với mọi x c)f'(x)=0 có 2 nghiệm cùng âm d)f'(x)=0 có nghiệm thỏa mãn x1+2x2=1
Cho hs
\(f\left(x\right)=-\dfrac{mx^3}{3}+3x^2-mx+1\)
tìm m để
a) \(f'\left(x\right)\le0,\forall x\in R\)
b) pt\(f'\left(x\right)=0\) có 2 nghiệm âm phân biệt