Chọn đáp án B
Yêu cầu bài toán ⇔ f(x) = 0 có ba nghiệm phân biệt (*)
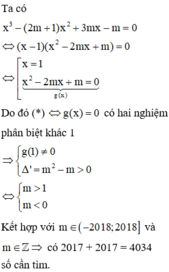
Chọn đáp án B
Yêu cầu bài toán ⇔ f(x) = 0 có ba nghiệm phân biệt (*)
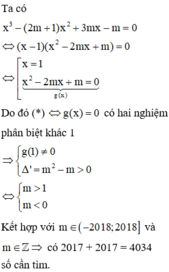
Cho hàm số f x m = x 3 - 2 m + 1 x 2 + 3 m x - m có đồ thị C m . Có bao nhiêu giá trị nguyên của tham số m thuộc [-2018;2018] để đồ thị C m có hai điểm cực trị nằm khác phía so với trục hoành.
A. 4033
B. 4034
C. 4035
D. 4036
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 - m + 1 x 2 + m 2 - 2 x - m 2 + 3 có hai điểm cực trị và hai điểm cực trị đó nằm về cùng một phía đối với trục hoành?
A. 4
B. 1
C. 3
D.
Cho hàm số y = x 3 + 3 m x 2 − m có đồ thị (C). Tất cả các giá trị của tham số thực m để (C) có hai điểm cực trị nằm về cùng một phía so với trục hoành là
A. m < − 1 2 h o ặ c m > 1 2
B. − 1 2 < m < 1 2 v à m ≠ 0
C. 0 < m < 1 2
D. − 1 2 < m ≤ 0
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 − 8 x 2 + ( m 2 + 11 ) x - 2m 2 + 2 có hai điểm cực trị nằm về hai phía của trục Ox.
A. 4
B. 5
C. 6
D. 7
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây: có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 2018 ) + m 2 có 5 điểm cực trị
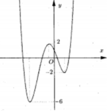
B. 1
C. 2
D. 3
Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y = x 3 - 5 2 x 2 - 2 x + 1 - m có hai điểm cực trị nằm về hai phía trục hoành?
A. 6.
B. 4.
C. 5.
D. 3.
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B và A B = 7 4 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số y = f ( x ) - g ( x ) + m có đúng 5 điểm cực trị?
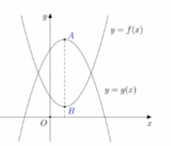
A. 1
B. 3
C. 4
D. 6
Có bao nhiêu giá trị nguyên dương của tham số m để trên đồ thị hàm số C m : y = 1 3 x 3 + m x 2 + 2 m - 3 x + 2018 có hai điểm nằm về phía của trục tung mà tiếp tuyến của C m tại hai điểm đó cùng vuông góc với đường thẳng d : x + 2 y - 5 = 0 ?
A. 3
B. 0
C. 2
D. 1
Cho hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 có đồ thị là (Cm) với m là tham số. Có bao nhiêu giá trị của m nguyên trong đoạn [–10;100] để (Cm) cắt trục hoành tại ba điểm phân biệt A(2;0), B, C sao cho trong hai điểm B, C có một điểm nằm trong và một điểm nằm ngoài đường tròn có phương trình x2 + y2 = 1?
A. 109
B. 108
C. 18
D. 19