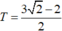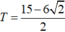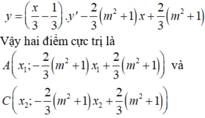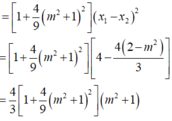Các câu hỏi tương tự
Tìm giá trị tham số m để đồ thị hàm số
y
x
4
-
2
(
m
+
1
)
x
2
+
2
m
+
3
có ba điểm cực trị A,B ,C sao cho trục hoành ch...
Đọc tiếp
Tìm giá trị tham số m để đồ thị hàm số y = x 4 - 2 ( m + 1 ) x 2 + 2 m + 3 có ba điểm cực trị A,B ,C sao cho trục hoành chia tam giác ABC thành một tam giác và một hình thang biết rằng tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4 9
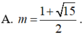
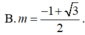
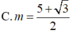
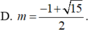
Đồ thị hàm số
y
x
4
-
2
m
2
x
2
+
m
2
(m là tham số) có ba điểm cực trị A, B, C sao cho bốn điểm A, B, C, O là bốn đỉnh của hình thoi (O là gốc toạ độ) khi và chỉ khi
Đọc tiếp
Đồ thị hàm số y = x 4 - 2 m 2 x 2 + m 2 (m là tham số) có ba điểm cực trị A, B, C sao cho bốn điểm A, B, C, O là bốn đỉnh của hình thoi (O là gốc toạ độ) khi và chỉ khi
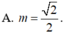
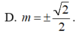
Cho hàm số ,m là tham số. Biết rằng đồ thị hàm số cắt trục hoành tại ba điểm phân biệt có hoành độ là a, b, c. Tính giá trị biểu thức A. 0 B.
1
3
C. 29-3m D. 3-m
Đọc tiếp
Cho hàm số 
,m là tham số. Biết rằng đồ thị hàm số cắt trục hoành tại ba điểm phân biệt có hoành độ là a, b, c. Tính giá trị biểu thức 
A. 0
B. 1 3
C. 29-3m
D. 3-m
Cho hàm số
y
x
4
-
m
x
2
+
2
m
-
1
có đồ thị là
(
C
m
)
. Tìm tất cả các giá trị của m để
(
C
m
)
có ba điểm cực trị cùng với gốc tọa độ tạo thành bốn đỉnh của...
Đọc tiếp
Cho hàm số y = x 4 - m x 2 + 2 m - 1 có đồ thị là ( C m ) . Tìm tất cả các giá trị của m để ( C m ) có ba điểm cực trị cùng với gốc tọa độ tạo thành bốn đỉnh của một hình thoi.
Cho hàm số y = x3 + 3mx2 + (m + 1)x + 1 (1), m là tham số thực. Tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x = -1 đi qua điểm A(1; 2).
A: 1
B: -1
C: 3/4
D: 5/8
Cho hàm số yf(x) và yg(x) là hai hàm liên tục trên
ℝ
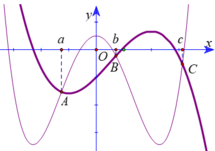
có đồ thị hàm số y f (x) là đường cong nét đậm và y g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của yf (x) và yg(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) f(x) - g(x) trên đoạn [a;c]?
Đọc tiếp
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số
y
x
2
+
m
4
-
x
2
+
m
-
7
có điểm chung với trục hoành là [a;b] (với a;b
∈...
Đọc tiếp
Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = x 2 + m 4 - x 2 + m - 7 có điểm chung với trục hoành là [a;b] (với a;b ∈ ℝ ). Tính giá trị của S = 2a + b.
A. S = 19 3
B. S = 7
C. S = 5
D. S = 23 3
Cho hàm số
y
x
4
-
2
m
x
2
+
1
-
m
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm. A. m 1 B. m 2 C. m 0 D. m -1
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm.
A. m = 1
B. m = 2
C. m = 0
D. m = -1
Tìm m để đường thẳng
d
:
y
-
1
cắt đồ thị (C) của hàm số
y
x
4
-
(
3
m
+
2
)
x
2...
Đọc tiếp
Tìm m để đường thẳng d : y = - 1 cắt đồ thị (C) của hàm số y = x 4 - ( 3 m + 2 ) x 2 + 3 m tại bốn điểm phân biệt có hoành độ nhỏ hơn 2
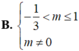
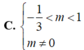
