Chọn A.
Phương pháp:
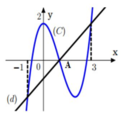
Gọi hàm số cần tìm là y = f x = a x 3 + b x 2 + c x + d
Xác định các điểm thuộc đồ thị hàm số rồi thay tọa độ vào hàm số để được hệ bốn ẩn
Giải hệ ta tìm được a;b;c;d . Từ đó tìm nghiệm phương trình f(x)=0 .


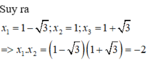
Chọn A.
Phương pháp:
Gọi hàm số cần tìm là y = f x = a x 3 + b x 2 + c x + d
Xác định các điểm thuộc đồ thị hàm số rồi thay tọa độ vào hàm số để được hệ bốn ẩn
Giải hệ ta tìm được a;b;c;d . Từ đó tìm nghiệm phương trình f(x)=0 .


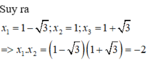

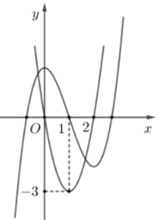
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
A. 0
B. -6
C. -7
D. -5
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2
Cho hàm số bậc 3:y=f(x) có đồ thị như hình vẽ.
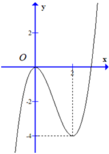
Xét hàm số g(x)=f[(x)]. Trong các mệnh đề dưới đây:
g(x) đồng biến trên (-∞;0) và (2;+∞).
Hàm số g(x) có bốn điểm cực trị.
m a x - 1 ; 1 g x = 0 .
Phương trình g(x)=0 có ba nghiệm.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 1.
D. 4.
Cho hàm số bậc ba y = f ( x ) có đồ thị như hình vẽ.
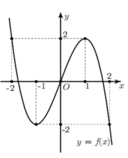
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;9] sao cho bất phương trình 2 f 2 ( x ) + f ( x ) − m − 16.2 f 2 ( x ) − f ( x ) − m − 4 f ( x ) + 16 < 0 có nghiệm x ∈ ( − 1 ; 1 ) ?
A. 6
B. 8
C. 5
D. 7
Cho đồ thị hàm số y=f (x) như hình vẽ. Tìm tất cả các giá trị thực m để phương trình f(x) +1= m có ba nghiệm phân biệt
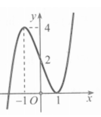
A. 0 < m < 5
B. 1 < m < 5
C. - 1 < m < 4
D. 0 < m < 4
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
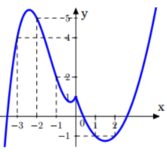
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Cho hàm số y = f(x) liên tục trên R có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của m để phương trình |f(x−2)+1| − m = 0 có 8 nghiệm phân biệt.

A. 0
B. 2.
C. 1.
D. 2.
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
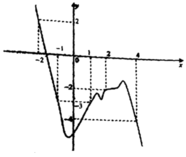
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình | f ( x ) | + m - 1 = 0 có 3 nghiệm phân biệt là
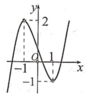
A. m=1
B. m=2
C. m = ± 1
D. m=0