Các câu hỏi tương tự
Cho hàm số
y
1
3
x
3
-
2
x
2
+
2
x
+
1
C
. Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h. A.
h
2
B.
h
4
2
3...
Đọc tiếp
Cho hàm số y = 1 3 x 3 - 2 x 2 + 2 x + 1 C . Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y = x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.
A. h = 2
B. h = 4 2 3
C. h = 2 3
D. h = 2 2 3
Đường thẳng d:yx-3 cắt đồ thị (C) của hàm số
y
x
+
1
x
-
2
tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng
△
:
x
-
y
0
Tính dd1+d A. B. C. d 6 D.
Đọc tiếp
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:y −
x
3
+ 3x + 1b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:y
(
x
+
1
)
3
− 3x − 4c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
(
x
+
1...
Đọc tiếp
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = − x 3 + 3x + 1
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:
y = ( x + 1 ) 3 − 3x − 4
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
( x + 1 ) 3 = 3x + m
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng
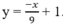
Cho hàm số
y
a
x
4
+
b
x
2
+
c
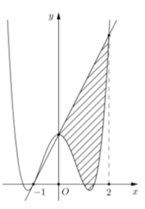
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Gọi (C) là đồ thị của hàm số
y
x
4
+
x
Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng d:x+5y0 có phương trình là A. B. C. D.
Đọc tiếp
Gọi (C) là đồ thị của hàm số y = x 4 + x Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng d:x+5y=0 có phương trình là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y 2x3-3x2+1 có đồ thị và đường thẳng d: yx-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là A. BC
30
2
B. BC
34
2
C. BC
3
2
2
D. BC
14
2
Đọc tiếp
Cho hàm số y= 2x3-3x2+1 có đồ thị và đường thẳng d: y=x-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là
A. BC= 30 2
B. BC= 34 2
C. BC= 3 2 2
D. BC= 14 2
Cho đồ thị
(
C
)
:
y
2
x
-
3
x
-
2
và đường thẳng (d): 5x + y - 1 0 . Goi k là số tiếp tuyến của (C) vuông góc với (d). Xác định k.
Đọc tiếp
Cho đồ thị ( C ) : y = 2 x - 3 x - 2 và đường thẳng (d): 5x + y - 1 = 0 . Goi k là số tiếp tuyến của (C) vuông góc với (d). Xác định k.
![]()
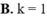
![]()
![]()
Cho hàm số
y
-
x
+
1
2
x
-
1
có đồ thị là (C) , đường thẳng d: yx+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất. A. m-1. B.m-2 . C. m3 . D. m-5.
Đọc tiếp
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y=x+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất.
A. m=-1.
B.m=-2 .
C. m=3 .
D. m=-5.
Cho hàm số
y
-
x
+
1
2
x
-
1
có đồ thị là (C) , đường thẳng d: y x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất. A. -2 B. -1 C. 1 D. 2
Đọc tiếp
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất.
A. -2
B. -1
C. 1
D. 2


